
| 小狗件数(单位:个) | 小汽车个数(单位:个) | 总时间(单位:分) | 总工资(单位:元) |
| 1 | 1 | 35 | 2.80 |
| 2 | 2 | 70 | 5.60 |
| 3 | 2 | 85 | 6.65 |
分析 (1)由图知:生产1个小狗用的时间+生产1个小汽车用的时间=35分钟;生产3个小狗用的时间+生产2个小汽车用的时间=85分钟;由此可列出方程组来求出制作一个小狗和一辆小汽车各需要多少时间;
(2)我们可通过:生产1个小狗的计件工资+生产1个小汽车的计件工资=2.8元;生产3个小狗的计件工资+生产2个小汽车的计件工资=6.65元;来列方程组求出制作一个小狗和一辆小汽车的计件工资各是多少元;
(3)设生产小狗x只,生产小汽车y辆,首先根据时间关系,列出等式用含有y的代数式表示出y,再根据“晓云想二月份领工资不少于1115元”列出不等式,进而得解;
(4)根据生产小狗的数量与生产小汽车的数量之间的关系,以及“计件工资每月下来不少于900元”列出不等式,进而得解.
解答 解:(1)设生产每个小狗所需时间为m分钟,生产每个小汽车所需时间为n分钟,
由题意可知:$\left\{\begin{array}{l}{m+n=35}\\{3m+2n=85}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=15}\\{n=20}\end{array}\right.$,
答:制作1个小狗所需时间为15分钟,制作1辆小汽车所需时间为20分钟;
(2)设生产每个小狗计件工资为a元,生产每个小汽车计件工资为b元,由题意可知:
$\left\{\begin{array}{l}{a+b=2.8}\\{3a+2b=6.65}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1.05}\\{b=1.75}\end{array}\right.$,
答:制作1个限购哦的计件工资是1.05元,制作1辆小汽车计件工资为1.75元;
(3)设生产小狗x只,生产小汽车y辆,据题意得:
15x+20y=25×8×60,
∴x=800-$\frac{4}{3}y$,
∵工资不少于1115元,
∴$1.05(800-\frac{4}{3}y)+1.75y+100≥1115$,
解得:y≥500,
当y=500时,x=$\frac{400}{3}$,不符合题意,舍去;
当y=501时,x=132,符合题意,
∴二月份至少需要生产小汽车501辆;
(4)设生产小狗x只,生产小汽车y辆,
∴x≥ky;
由(3)知x=$800-\frac{4}{3}y$,
1.05(800$-\frac{4}{3}y$)+1.75y≥900,
∴y≤$\frac{2400}{k+4}$或y≥$\frac{1200}{7}$,
∴当k=4,5,6,7,8,9,10,11,12时广告有欺诈行为.
点评 本题主要考查了二元一次方程组的实际应用,根据题意列出二元一次方程组是解题的关键;还考查了一元一次不等式的实际应用,是经常考查的题目,注意总结.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
| A | B | C | |
| 笔试 | 85 | 95 | 90 |
| 口试 | 90 | 80 | 85 |
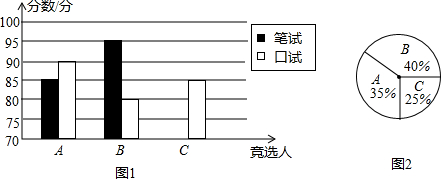
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,将-4,-3,-2,-1,0,1,2,3,4这9个数字填入图中的9个方格中,使得方格中,每行,每列,以及对角线上的3个数字之和都为0.
如图,将-4,-3,-2,-1,0,1,2,3,4这9个数字填入图中的9个方格中,使得方格中,每行,每列,以及对角线上的3个数字之和都为0.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
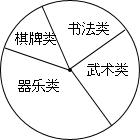 某校学生会准备调查七年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数,他们采用了最为合理的调查方法收集数据,并绘制了如图所示的统计表和扇形统计图
某校学生会准备调查七年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数,他们采用了最为合理的调查方法收集数据,并绘制了如图所示的统计表和扇形统计图| 类别 | 频数(人数) | 频率 |
| 武术类 | 25 | 0.25 |
| 书画类 | 20 | 0.20 |
| 棋牌类 | 15 | b |
| 器乐类 | 40 | 0.40 |
| 合计 | a | 1.00 |
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
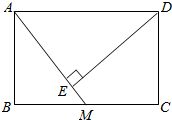 矩形ABCD中,M是BC的中点,DE⊥AM,E是垂足.
矩形ABCD中,M是BC的中点,DE⊥AM,E是垂足.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
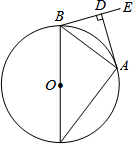 如图,已知:⊙O为△ABC的外接圆,BC为⊙O的直径,BA平分∠CBE,AD⊥BE,垂足为D.
如图,已知:⊙O为△ABC的外接圆,BC为⊙O的直径,BA平分∠CBE,AD⊥BE,垂足为D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com