
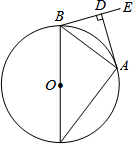
 如图,已知:⊙O为△ABC的外接圆,BC为⊙O的直径,BA平分∠CBE,AD⊥BE,垂足为D.
如图,已知:⊙O为△ABC的外接圆,BC为⊙O的直径,BA平分∠CBE,AD⊥BE,垂足为D.分析 (1)要证AD是⊙O的切线,连接OA,只证∠DAO=90°即可.
(2)根据三角函数的知识可求出AB,从而根据勾股定理求出BC的长,得出⊙O的直径.
解答 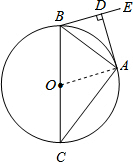 (1)略(2)10
(1)略(2)10
(1)证明:连接OA;
∵BC为⊙O的直径,BA平分∠CBE,AD⊥BE,
∴∠ADB=∠BAC=90°,∠DBA=∠CBA;
∵OA=OC,
∴∠OAC=∠OCA,
∴∠DAO=∠DAB+∠BAO=∠BAO+∠OAC=90°,
∴DA为⊙O的切线.
(2)解:∵∠DBA=∠CBA,tan∠ABD=$\frac{4}{3}$,AC=8,
∴tan∠CBA=$\frac{4}{3}$,
∴AB=$\frac{AC}{tan∠CBA}$=$\frac{8}{\frac{4}{3}}$=6,
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∴⊙O的直径BC为10.
点评 本题考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.同时考查了三角函数的知识.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
| 小狗件数(单位:个) | 小汽车个数(单位:个) | 总时间(单位:分) | 总工资(单位:元) |
| 1 | 1 | 35 | 2.80 |
| 2 | 2 | 70 | 5.60 |
| 3 | 2 | 85 | 6.65 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
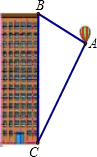 如图,热气球的探测器显示,从热气球看一栋高楼顶部的仰角为35.6°,看这栋高楼底部的俯角的正切值为2,热气球与高楼的水平距离为90米,这栋高楼有多高(结果精确到0.1米.参考数据:sin35.6°=0.582,cos35.6°=0.813,tan35.6°=0.716)?
如图,热气球的探测器显示,从热气球看一栋高楼顶部的仰角为35.6°,看这栋高楼底部的俯角的正切值为2,热气球与高楼的水平距离为90米,这栋高楼有多高(结果精确到0.1米.参考数据:sin35.6°=0.582,cos35.6°=0.813,tan35.6°=0.716)?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com