
【题目】如图,抛物线y=ax2+3x+c经过A(﹣1,0),B(4,0)两点,与y轴交于点C.
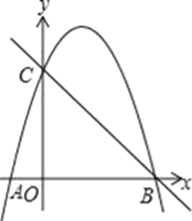
(1)求抛物线的解析式;
(2)若点P在第一象限的抛物线上,且点P的横坐标为t,过点P向x轴作垂线交直线BC于点Q,设线段PQ的长为m,求m与t之间的函数关系式,并求出m的最大值;
(3)在(2)的条件下,抛物线上点D(不与C重合)的纵坐标为m的最大值,在x轴上找一点E,使点B、C、D、E为顶点的四边形是平行四边形,请直接写出E点坐标.
【答案】(1)![]() ;(2)
;(2)![]() ,当
,当![]() 时,
时,![]() 的最大值为4;(3)
的最大值为4;(3)![]() 或
或![]()
【解析】
(1)将点![]() 、
、![]() 的坐标代入抛物线的解析式得到关于
的坐标代入抛物线的解析式得到关于![]() 、
、![]() 的方程组,从而可求得
的方程组,从而可求得![]() 、
、![]() 的值;
的值;
(2)先求得点![]() 的坐标,然后依据待定系数法求得直线
的坐标,然后依据待定系数法求得直线![]() 的解析式,由直线可抛物线的解析式可知
的解析式,由直线可抛物线的解析式可知![]() ,
,![]() ,从而可求得
,从而可求得![]() 与
与![]() 的关系式,最后依据配方法可求得
的关系式,最后依据配方法可求得![]() 的最大值;
的最大值;
(3)将![]() 代入抛物线的解析式求得点
代入抛物线的解析式求得点![]() 的坐标,依据一组对边平行且相等的四边形是平行四边形可得到
的坐标,依据一组对边平行且相等的四边形是平行四边形可得到![]() 时,
时,![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,从而可求得点
为顶点的四边形是平行四边形,从而可求得点![]() 的坐标.
的坐标.
解(1)![]() 抛物线
抛物线![]() 经过
经过![]() ,
,![]() 两点,
两点,
![]()
![]() .
.
解得:![]() ,
,![]() .
.
![]() 抛物线的解析式为
抛物线的解析式为![]() .
.
(2)![]() 将
将![]() 代入抛物线的解析式得:
代入抛物线的解析式得:![]() ,
,
![]() .
.
设直线![]() 的解析式为
的解析式为![]() .
.
![]() 将
将![]() ,
,![]() 代入得:
代入得:![]() ,解得:
,解得:![]() ,
,![]()
![]() 直线
直线![]() 的解析式为:
的解析式为:![]() .
.
过点![]() 作
作![]() 的垂线
的垂线![]() 交
交![]() 于点Q,如图所示:
于点Q,如图所示:

![]() 点
点![]() 的横坐标为
的横坐标为![]() ,
,
![]() ,
,![]() .
.
![]() .
.
![]() .
.
![]() 当
当![]() 时,
时,![]() 的最大值为4.
的最大值为4.
(3)将![]() 代入抛物线的解析式得:
代入抛物线的解析式得:![]() .
.
解得:![]() ,
,![]() .
.
![]() 点
点![]() 与点
与点![]() 不重合,
不重合,
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
又![]()
![]() 轴,
轴,![]() .
.
![]() 当
当![]() 时,
时,![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.
![]() 点
点![]() 或
或![]() .
.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
【题目】《孙子算经》是中国传统数学最重要的著作,约成书于四、五世纪.现在传本的《孙子算经》共三卷.卷上叙述算筹记数的纵横相间制度和筹算乘除法则;卷中举例说明筹算分数算法和筹算开平方法;卷下记录算题,不但提供了答案,而且还给出了解法.其中记载:“今有木,不知长短.引绳度之,余绳四尺五,屈绳量之,不足一尺.问木长几何?”
译文:“用一根绳子去量一根长木,绳子还剩余4.5尺,将绳子对折再量长木,长木还剩余1尺,问长木长多少尺?”
请解答上述问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:△ABC是等边三角形,AB=12,E是AC中点,D是直线BC上一动点,线段ED绕点E逆时针旋转90°,得线段EF,当点D运动时,则线段AF的最小值为_____.
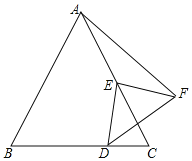
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全民健身运动已成为一种时尚,为了了解我市居民健身运动的情况,某健身馆的工作人员开展了一项问卷调查,问卷包括五个项目:A:健身房运动;B:跳广场舞;C:参加暴走团;D:散布;E:不运动.
以下是根据调查结果绘制的统计图表的一部分.
运动形式 | A | B | C | D | E |
人数 | 12 | 30 | m | 54 | 9 |
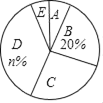
请你根据以上信息,回答下列问题:
(1)接受问卷调查的共有 人,图表中的m= ,n= ;
(2)统计图中,A类所对应的扇形圆心角的度数为 ;
(3)根据调查结果,我市市民最喜爱的运动方式是 ,不运动的市民所占的百分比是 ;
(4)郑州市碧沙岗公园是附近市民喜爱的运动场所之一,每晚都有“暴走团”活动,若最邻近的某社区约有1500人,那么估计一下该社区参加碧沙岗“暴走团”的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知开口向上的抛物线![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() ,函数值
,函数值![]() 的最小值是
的最小值是![]() .
.
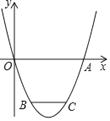
(1)求抛物线的解析式.
(2)点![]() 为抛物线上的点,并在对称轴的左侧.作
为抛物线上的点,并在对称轴的左侧.作![]() 轴交抛物线于点
轴交抛物线于点![]() ,连结
,连结![]() ,
,![]() ,且
,且![]() .
.
①求![]() 的值.
的值.
②若点![]() 在线段
在线段![]() 上,以点
上,以点![]() 为圆心,
为圆心,![]() 为半径画圆.当
为半径画圆.当![]() 和
和![]() 的一边相切时,求点
的一边相切时,求点![]() 的横坐标.
的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
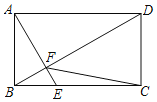
【题目】如图,在矩形ABCD中,点E是BC边上的一点,且AE⊥BD,垂足为点F,∠DAE=2∠BAE.
(1)求证:BF:DF=1:3;
(2)若四边形EFDC的面积为11,求△CEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年5月,某大型商业集团随机抽取所属的部分商业连锁店进行评估,将抽取的各商业连锁店按照评估成绩分成了![]() 、
、![]() 、
、![]() 、
、![]() 四个等级,并绘制了如下不完整的扇形统计图和条形统计图.
四个等级,并绘制了如下不完整的扇形统计图和条形统计图.
根据以上信息,解答下列问题:
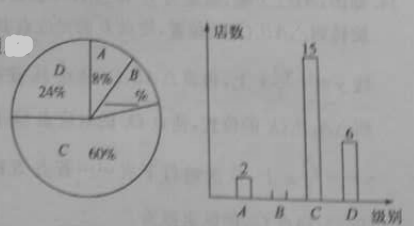
(1)本次评估随机抽取了多少家商业连锁店?
(2)请补充完整扇形统计图和条形统计图,并在图中标注相应数据;
(3)从![]() 、
、![]() 两个等级的商业连锁店中任选2家介绍营销经验,求其中至少有一家是
两个等级的商业连锁店中任选2家介绍营销经验,求其中至少有一家是![]() 等级的概率.
等级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
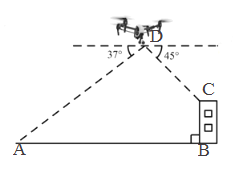
【题目】某无人机兴趣小组在操场上开展活动(如图),此时无人机在离地面30米的D处,无人机测得操控者A的俯角为37°,测得点C处的俯角为45°.又经过人工测量操控者A和教学楼BC距离为57米,求教学楼BC的高度.(注:点A,B,C,D都在同一平面上.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com