
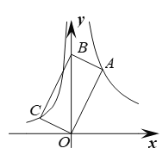
【题目】如图,四边形ABCO为矩形,点A在反比例函数y=![]() (x>0)的图象上,点C在反比例函数y=-
(x>0)的图象上,点C在反比例函数y=-![]() (x<0)的图象上,若点B在y轴上,则点A的坐标为_______.
(x<0)的图象上,若点B在y轴上,则点A的坐标为_______.
【答案】![]()
【解析】
连接AC交BO于E,过点C作CM⊥x轴,垂足为M,过点A作AN⊥x轴,垂足为N.先通过矩形的性质得到CE=AE,进一步得到MO=NO,设A(a,![]() ),则C点坐标为(-a,
),则C点坐标为(-a,![]() );然后在说明△CMO∽△ONA,最后根据相似三角形的性质列方程解答即可.
);然后在说明△CMO∽△ONA,最后根据相似三角形的性质列方程解答即可.
解:连接AC交BO于E,过点C作CM⊥x轴,垂足为M,过点A作AN⊥x轴,垂足为N.
∵四边形ABCO是矩形
∴CE=BE=AE=OE,∠AOC=90°
∵点E在y轴上
∴∠CMO=∠EON=∠ANO=90°
∴CM∥EO∥AN
∵CE=AE
∴MO=NO
∵点A在反比例函数y=![]() 的图像上,
的图像上,
∴设A(a,![]() )
)
∴MO=NO=a
又∵点C在反比例函数y=-![]() 的图象上
的图象上
∴C(-a,![]() )
)
∴CM=![]()
又∵∠COA=90°
∴∠AON + ∠COM=90°,
又∵∠MCO+ ∠COM=90,
∴∠AON=∠MCO,
又∵∠CMO=∠ANO=90°
∴△CMO∽△ONA,
∴![]() ,
,
∴OM·ON=CM·AN,
∴a2=![]() ·
·![]() =
=![]()
∴a2 =2
∵a>0,
∴a=![]() ,
,![]() =
=![]() =2
=2![]()
故答案为![]() .
.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,点
两点,点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)![]() _________,
_________,![]() _________;
_________;
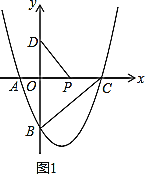
(2)如图1,![]() 是
是![]() 轴上一动点,点
轴上一动点,点![]() 在
在![]() 轴上,连接
轴上,连接![]() ,求
,求![]() 的最小值;
的最小值;
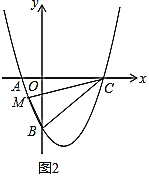
(3)如图2,点![]() 在抛物线上,若
在抛物线上,若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加快“智慧校园”建设,某市准备为试点学校采购一批![]() 、
、![]() 两种型号的一体机,经过市场调查发现,今年每套
两种型号的一体机,经过市场调查发现,今年每套![]() 型一体机的价格比每套
型一体机的价格比每套![]() 型一体机的价格多0.6万元,且用960万元恰好能购买500套
型一体机的价格多0.6万元,且用960万元恰好能购买500套![]() 型一体机和200套
型一体机和200套![]() 型一体机.
型一体机.
(1)求今年每套![]() 型、
型、![]() 型一体机的价格各是多少万元
型一体机的价格各是多少万元
(2)该市明年计划采购![]() 型、
型、![]() 型一体机1100套,考虑物价因素,预计明年每套
型一体机1100套,考虑物价因素,预计明年每套![]() 型一体机的价格比今年上涨25%,每套
型一体机的价格比今年上涨25%,每套![]() 型一体机的价格不变,若购买
型一体机的价格不变,若购买![]() 型一体机的总费用不低于购买
型一体机的总费用不低于购买![]() 型一体机的总费用,那么该市明年至少需要投入多少万元才能完成采购计划?
型一体机的总费用,那么该市明年至少需要投入多少万元才能完成采购计划?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个药店销售同一种口罩,在甲药店,不论一次购买数量是多少,价格均为3元/个;在乙药店,一次性购买数量不超过100个时,价格为3.5元/个;一次性购买数量超过100个时,其中100个的价格仍为3.5元/个,超过100个的部分的价格为2.5元/个.
(1)根据题意填表:
一次性购买数量(个) | 50 | 100 | 150 |
甲药店花费(元) |
| 300 |
|
乙药店花费(元) |
| 300 |
|
(2)当一次性购买多少个口罩时,在乙药店购买比在甲药店购买可以节约100元?
查看答案和解析>>
科目:初中数学 来源: 题型:
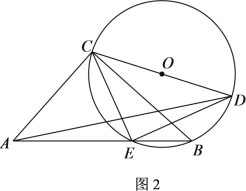
【题目】如图1,点E为△ABC边AB上的一点,⊙O为△BCE的外接圆,点D为![]() 上任意一点.若AE=AC=2n,BC=n2-1,BE=n2-2n+1 .(n≥2,且n为正整数) .
上任意一点.若AE=AC=2n,BC=n2-1,BE=n2-2n+1 .(n≥2,且n为正整数) .
(1)求证:∠CAE+∠CDE=90°;
(2)①如图2,当CD过圆心O时,①将△ACD绕点A顺时针旋转得△AEF,连接DF,请补全图形,猜想CD、DE、DF之间的数量关系,并证明你的猜想;②若n=3,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中有标号为1,2,3,4的四个小球,除数字不同外,小球没有任何区别,摸球前先搅拌均匀,每次摸一个球
(1)摸出一个球,摸到标号为偶数的概率为 .
(2)从袋中不放回地摸两次,用列表或树状图求出两球标号数字为一奇一偶的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区域平面示意图如图,点O在河的一侧,AC和BC表示两条互相垂直的公路.甲勘测员在A处测得点O位于北偏东45°,乙勘测员在B处测得点O位于南偏西73.7°,测得AC=840m,BC=500m.请求出点O到BC的距离.参考数据:sin73.7°≈![]() ,cos73.7°≈
,cos73.7°≈![]() ,tan73.7°≈
,tan73.7°≈![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
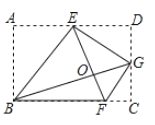
【题目】将矩形ABCD按如图所示的方式折叠,BE,EG,FG为折痕,若顶点A,C,D都落在点O处,且点B,O,G在同一条直线上,同时点E,O,F在另一条直线上,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com