练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，从圆O外一点P引圆O的两条切线PA，PB，切点分别为A，B．如果∠APB=60°，PA=8，那么弦AB的长是（　　）

    A．4       B．8       C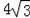． D．


    B【考点】切线长定理；等边三角形的判定与性质．

    【专题】压轴题．

    【分析】根据切线长定理知PA=PB，而∠P=60°，所以△PAB是等边三角形，由此求得弦AB的长．

    【解答】解：∵PA、PB都是⊙O的切线，

    ∴PA=PB，

    又∵∠P=60°，

    ∴△PAB是等边三角形，即AB=PA=8，

    故选B．

    【点评】此题主要考查的是切线长定理以及等边三角形的判定．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


     “水是生命之源”，某城市自来水公司为了鼓励居民节约用水，规定按以下标准收取水费：

    用水量/月

    单价（元/m3）

    不超过20m3

    2.8

    超过20m3的部分

    3.8

    另：每立方米用水加收0.2元的城市污水处理费

    （1）如果1月份某用户用水量为19m3，那么该用户1月份应该缴纳水费__________元．

    （2）某用户2月份共缴纳水费80元，那么该用户2月份用水多少m3？

    （3）若该用户水表3月份出了故障，只有70%的用水量记入水表中，这样该用户在3月份只缴纳了58.8元水费，问该用户3月份实际应该缴纳水费多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    PM 2.5是指大气中直径小于或等于0.0000025m的颗粒物，将0.0000025用科学记数法表示为　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在△ABC中，∠C=90°，点D、E分别是边A以、BC上的点，点P是一动点，连接PD、PE，∠PDA=∠1，∠PEB=∠2，∠DPE=∠α．

    （1）如图1所示，若点P在线段AB上，且∠α=40°，则∠1+∠2=　130　°；

    （2）如图2所示，若点P在边AB上运动，则∠α、∠1、∠2之间的关系为有何数量关系；猜想结论并说明理由；

    （3）如图3所示，若点P运动到边AB的延长线上，则∠α、∠1、∠2之间有何数量关系？猜想结论并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一次函数y=2x﹣3的图象不经过（　　）

    A．第一象限 B．第二象限  C．第三象限 D．第四象限

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若把代数式x2﹣2x﹣3化为（x﹣m）2+k的形式，其中m，k为常数，则m+k=　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


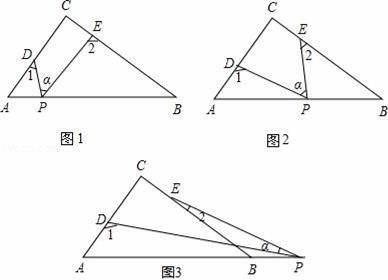
    在▱ABCD中，∠BAD的平分线交直线BC于点E，交直线DC于点F．

    （1）在图1中证明CE=CF；

    （2）若∠ABC=90°，G是EF的中点（如图2），直接写出∠BDG的度数；

    （3）若∠ABC=120°，FG∥CE，FG=CE，分别连接DB、DG（如图3），求∠BDG的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    小明与小刚规定了一种新运算*：若a、b是有理数，则a*b=3a﹣2b．小明计算出2*5=﹣4，请你帮小刚计算2*（﹣5）=　　　　　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


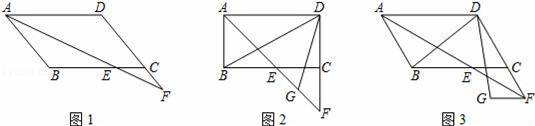
    有理数a、b在数轴上表示的点如图，则a、﹣a、b、﹣b大小关系是（　　）

    A．﹣b＞a＞﹣a＞b     B．a＞﹣a＞b＞﹣b      C．b＞a＞﹣b＞﹣a     D．﹣b＜a＜﹣a＜b

    　

    查看答案和解析>>

    同步练习册答案