
��ˮ������֮Դ����ij��������ˮ��˾Ϊ�˹��������Լ��ˮ���涨�����±���ȡˮ�ѣ�
| ��ˮ��/�� | ���ۣ�Ԫ/m3�� |
| ������20m3 | 2.8 |
| ����20m3�IJ��� | 3.8 |
| ����ÿ��������ˮ����0.2Ԫ�ij�����ˮ������ |
��1�����1�·�ij�û���ˮ��Ϊ19m3����ô���û�1�·�Ӧ�ý���ˮ��__________Ԫ��
��2��ij�û�2�·ݹ�����ˮ��80Ԫ����ô���û�2�·���ˮ����m3��
��3�������û�ˮ��3�·ݳ��˹��ϣ�ֻ��70%����ˮ������ˮ���У��������û���3�·�ֻ������58.8Ԫˮ�ѣ��ʸ��û�3�·�ʵ��Ӧ�ý���ˮ�Ѷ���Ԫ��
�����㡿һԪһ�η��̵�Ӧ�ã�
����������1�����û�1�·���ˮ��û�г���20m3��ֱ���õ��ۡ���ˮ�����ɣ�
��2������û�2�·���ˮxm3�������⣬��20��3+4����x﹣20��=80�����x��ֵ���ɣ�
��3����������û�3�·�ʵ����ˮam3��Ȼ�����a��ֵ�����ݱ���ˮ��������û�3�·�ʵ��Ӧ�ý���ˮ�ѣ�
����𡿽⣺��1�����ݱ������ݿ�֪��
���û�1�·�Ӧ�ý���ˮ��19��3=57Ԫ��
��2������û�2�·���ˮxm3�������⣬��20��3+4����x﹣20��=80��
��ã�x=25��
�𣺸��û�2�·���ˮ25m3��
��3������û�3�·�ʵ����ˮam3
��Ϊ58.8��20��3�����Ը��û��Ͻ�ˮ�ѵĵ���Ϊ3Ԫ/m3��
�����⣬��70%a��3=58.8��
��ã�a=28��
��Ϊ28��20��
���Ը��û�3�·�ʵ��Ӧ�ý���ˮ��Ϊ��20��3+4����28﹣20��=92Ԫ��
�𣺸��û�3�·�ʵ��Ӧ�ý���ˮ��92Ԫ��
�����������⿼���˵��ۡ�����=�ܼ۵�������ϵ�����ã���һԪһ�η��̽�ʵ����������ã�һԪһ�η��̵Ľⷨ�����ã����ʱ�ɵ��ۡ�����=�ܼ۵Ĺ�ϵ���������ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����1����2����3����4�������ABCDE����ǣ��ҡ�1=��2=��3=��4=70�㣬���AED�Ķ����ǣ�������
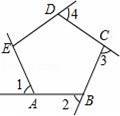

A��80�� B��100�� C��108�� D��110��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����֪��������ĺô�����ʵ�ϣ��������ںö�ط������ڣ��۲����е�ʽ��
152=1��2��100+25=225��
252=2��3��100+25=625��
352=3��4��100+25=1225��
��
��1������������ʽ��Ӧ���Ĺ�����գ�952=�� 5����
��2���������ʽ�����λ����ʮλ����Ϊa������һ����a�Ĵ���ʽ��ʾ������ ����
��3�����ּ�����Ҳ�����ƹ�Ӧ�ã�
�ٸ�λ������5����λ����ƽ������д��1952�ļ�������̼������
��ʮλ������ͬ���Ҹ�λ����֮����10��������λ����ɵ���ʽ����д��89��81�ļ�������̺ͽ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����ԲO��һ��P��ԲO����������PA��PB���е�ֱ�ΪA��B�������APB=60�㣬PA=8����ô��AB�ij��ǣ�������


A��4 B��8 C��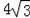
 D��
D��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com