
如图,点D是△ABC的边BC上任意一点,点E、F分别是线段AD、CE的中点,且△ABC的面积为16cm2,则△BEF的面积:__________cm2.
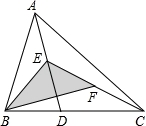
4cm2.
【考点】三角形的面积.
【分析】首先根据点E是线段AD的中点,三角形的中线将三角形分成面积相等的两部分,可得△BDE的面积等于三角形△ABE的面积,△CDE的面积△等于三角形ACE的面积,所以△BCE的面积等于△ABC的面积的一半;然后根据点F是线段CE的中点,可得△BEF的面积等于△BCE的面积的一半,据此用△BCE的面积除以2,求出△BEF的面积是多少即可.
【解答】解:∵AE=DE,
∴S△BDE=S△ABE,S△CDE=S△ACE,
∴S△BDE=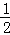 S△ABD,S△CDE=
S△ABD,S△CDE=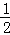 S△ACD,
S△ACD,
∴S△BCE=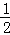 S△ABC=
S△ABC=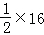 =8(cm2);
=8(cm2);
∵EF=CF,
∴SBEF=S△BCF,
∴S△BEF=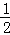 S△BCE=
S△BCE=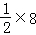 =4(cm2),
=4(cm2),
即△BEF的面积是4cm2.
故答案为:4.
【点评】此题主要考查了三角形的面积的求法,以及三角形的中线的特征,要熟练掌握,解答此题的关键要明确:三角形的中线将三角形分成面积相等的两部分.


科目:初中数学 来源: 题型:
某商场计划购进A,B两种新型节能台灯共100盏,这两种台灯的进价、售价如表所示:
| 类型 价格 | 进价(元/盏) | 售价(元/盏) |
| A型 | 30 | 45 |
| B型 | 50 | 70 |
(1)设商场购进A型节能台灯为x盏,销售完这批台灯时可获利为y元,求y关于x的函数解析式;
(2)若商场规定B型台灯的进货数量不超过A型台灯数量的3倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com