
����Ŀ��ij�̵꾭��һ�����۳ɱ�Ϊÿǧ��40Ԫ��ˮ��Ʒ�����г���������ÿǧ��50Ԫ���ۣ�һ�������۳�500kg�����۵���ÿ��2Ԫ�����������ͼ���20kg���������ˮ��Ʒ����������������⣺
��1�������۵��۶�Ϊÿǧ��55Ԫʱ������������������������
��2����Ʒ���������۳ɱ�������10000Ԫ������£�ʹ������������ﵽ8000Ԫ�����۵���ӦΪ���٣�
���𰸡���1��6750Ԫ����2����Ʒ���������۳ɱ�������10000Ԫ������£�ʹ������������ﵽ8000Ԫ�����۵���ӦΪ80Ԫ��
��������
��1�����ݡ����۵���ÿ��2Ԫ�����������ͼ���20ǧ�ˡ�����֪����������=500-�����۵���-50����![]() ���ɴ˿ɵó��ۼ�Ϊ55Ԫ/ǧ��ʱ������������Ȼ���������=ÿǧ�˵���������۵��������������������
���ɴ˿ɵó��ۼ�Ϊ55Ԫ/ǧ��ʱ������������Ȼ���������=ÿǧ�˵���������۵��������������������
��2�����۳ɱ�������10000Ԫ��������������10000��40=250kg�������������ʽ�����������8000ʱ���ۼۣ��Ӷ���������������������Ƚϵý��ۣ�
�⣺��1�������۵��۶�Ϊÿǧ��55Ԫʱ����������Ϊ��500����55��50����10��450��ǧ�ˣ���
��������������Ϊ����55��40����450��6750Ԫ��
��2������ˮ��Ʒ������10000��40��250kg������ΪxԪ��
��x��40��[500��10��x��50��]��8000��
��ã�x1��80��x2��60��
��x1��80ʱ������500��10��80��50����200kg��250kg���������⣬
��x2��60ʱ������500��10��60��50����400kg��250kg����ȥ��
����Ʒ���������۳ɱ�������10000Ԫ������£�ʹ������������ﵽ8000Ԫ�����۵���ӦΪ80Ԫ��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д� Ŀ�����ϵ�д�
Ŀ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
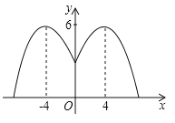
����Ŀ��ij����Ҫ��һ��Բ����ˮ�أ�����ˮ�ص����İ�װһ�������ˮͷ���߶�Ϊ![]() m�������ˮ���������߹켣�˶�����ͼ������������ˮƽ����4m���ﵽ��ߣ��߶�Ϊ6m��֮������ˮ�ر�Ե����ô�����ˮ�ص�ֱ��ABΪ____m��
m�������ˮ���������߹켣�˶�����ͼ������������ˮƽ����4m���ﵽ��ߣ��߶�Ϊ6m��֮������ˮ�ر�Ե����ô�����ˮ�ص�ֱ��ABΪ____m��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
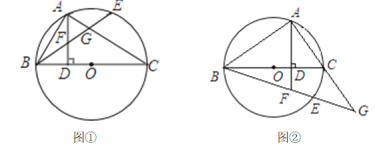
����Ŀ����ͼ�٣�BC�ǡ�O��ֱ������A�ڡ�O�ϣ�AD��BC����ΪD����AE=��AB��BE�ֱ�AD��AC�ڵ�F��G.
��1���ж���FAG����״����˵������.
��2����ͼ������E���A��ֱ��BC�����࣬BE��AC���ӳ��߽��ڵ�G��AD���ӳ��߽�BE�ڵ�F�������������䣨1���еĽ��ۻ���������˵������
��3���ڣ�2���������£���BG=26��BD-BF=7,��AB�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��������5�����ۣ���abc��0����4a+2b+c��0����2a+b=0����b2��4ac�� �� 3a+c��0��������ȷ�Ľ��۵��У� ��
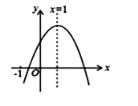
A.2��B.3��C.4��D.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A1��A2��A3������An��������y��x2ͼ���ϣ���B1��B2��B3������Bn��y���ϣ�����A1B0B1����A2B1B2��������AnBn��1Bn��Ϊ����ֱ�������Σ���B0������ԭ�㣩�����A2014B2013B2014��������_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
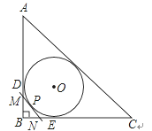
����Ŀ����ͼ��Rt��ABC������Բ��O����ֱ�DZ�AB��BC�ֱ������ڵ�D��E�����ӻ�DE���������˵�D��E������һ��P����O������MN��AB��BC�ֱ��ڵ�M��N������O�İ뾶Ϊ4cm����Rt��MBN���ܳ�Ϊ________cm.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���y=x+2��ͼ��ֱ�x�ᣬy����A��B���㣬��O1����OBΪ�߳���������OBCD���ĸ����㣬������P��Qͬʱ�ӵ�A�������ı���ABCD���˶������ж���P��ÿ��![]() ����λ���ȵ��ٶ���A��B��A�˶���ֹͣ������Q��ÿ��2����λ���ȵ��ٶ���A��O��D��C��B�˶���AO1��y����E�㣬P��Q�˶���ʱ��Ϊt���룩��
����λ���ȵ��ٶ���A��B��A�˶���ֹͣ������Q��ÿ��2����λ���ȵ��ٶ���A��O��D��C��B�˶���AO1��y����E�㣬P��Q�˶���ʱ��Ϊt���룩��
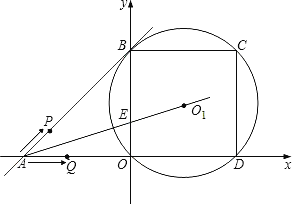
��1����E��������S��ABE��ֵ��
��2����̽����P��Q�ӿ�ʼ�˶���ֹͣ��ֱ��PQ����O1���ļ���λ�ù�ϵ���������Ӧ���˶�ʱ��t�ķ�Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
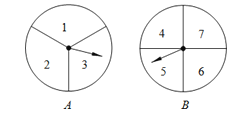
����Ŀ���ס�����������ͼ�������ָ���ȵ�ת��A��B����Ϸ����Ϸ�������£��ֱ�ת������ת�̣�ת��ֹͣ��ָ��ֱ�ָ��һ�����֣���ָ��ֹͣ�ڵȷ����ϣ���ô��תһ�Σ�ֱ��ָ��ָ��ijһ����Ϊֹ��������ָ������������ˣ�����������������ʤ���������ż�������һ�ʤ���������������⣺
��1�����б������״ͼ�ķ�����ʾ��Ϸ���п��ܳ��ֵĽ����
��2����ס������˻�ʤ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ı���ABCD��ƽ���ı��Σ����н����в���ȷ���ǣ�������

A. ��AB=BCʱ���ı���ABCD������
B. ��AC��BDʱ���ı���ABCD������
C. ����ABC=90��ʱ���ı���ABCD�Ǿ���
D. ��AC=BDʱ���ı���ABCD��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com