
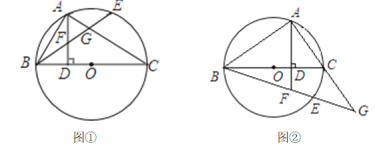
【题目】如图①,BC是⊙O的直径,点A在⊙O上,AD⊥BC垂足为D,弧AE=弧AB,BE分别交AD、AC于点F、G.
(1)判断△FAG的形状,并说明理由.
(2)如图②若点E与点A在直径BC的两侧,BE、AC的延长线交于点G,AD的延长线交BE于点F,其余条件不变(1)中的结论还成立吗?请说明理由
(3)在(2)的条件下,若BG=26,BD-BF=7,求AB的长。
【答案】(1)见解析;(2)见解析;(3)4![]() .
.
【解析】
(1)首先根据圆周角定理及垂直的定义得到∠BAD+∠CAD=90°,∠C+∠CAD=90°,从而得到∠BAD=∠C,然后利用等弧对等角等知识得到AF=BF,从而证得FA=FG,判定等腰三角形;
(2)成立,证明方法同(1);
(3)首先根据上题得到AF=BF=FG,从而利用已知条件得到FB=13,然后利用勾股定理得到BD=12,DF=5,从而求得AD=8,最后求得AB=4![]() .
.
解:(1)△FAG是等腰三角形,∵BC是⊙O的直径,∴∠BAC=90°,
∴∠ABE+∠AGB=90°,∵AD⊥BC ,∴∠ACB+∠DAC=90°,∵弧AE=弧AB,
∴∠ABE=∠ACB,∴∠AGB=∠DAC,∴△FAG是等腰三角形.
(2)成立.
∵BC是⊙O的直径,∴∠BAC=90°,
∴∠ABG+∠G=90°,∵AD⊥BC,∴∠ACB+∠CAF=90°,∵弧AE=弧AB,
∴∠ABG=∠ACB,∴∠G=∠CAF,∴△FAG是等腰三角形;
(3)由(2)中可得:AF=BF=FG,∵BG=26,∴BF=13,在Rt△BDF中,BD2 +DF2=BF2,∴BD2 +DF2=169,又∵BD -DF=7,解得BD=12,DF=5,∴AD=AF-DF=13-5=8,∴AB=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论中错误的是( )

A. b2>4ac
B. ax2+bx+c≥﹣6
C. 若点(﹣2,m),(﹣5,n)在抛物线上,则m>n
D. 关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的方程ax2﹣3x﹣1=0的两个不相等实数根均大于﹣1且小于0,则a的取值范围为( )
A. a>0B. ﹣2<a<﹣1C. ﹣![]() <a<﹣1D. ﹣
<a<﹣1D. ﹣![]() <a<﹣2
<a<﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(﹣1,0).一个电动玩具从坐标原点O出发,第一次跳跃到点P1.使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去,则点P2013的坐标为 .
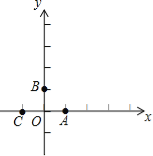
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC.
(1)请用圆规和直尺作△ABC的内切圆(要求保留作图痕迹,不必写作法和证明);
(2)若等边△ABC边长为2,求△ABC的内切圆的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了帮助贫困家庭脱困,精准扶贫小组帮助一农户建立如图所示的长方形养鸡场,长方形的面积为45m2(分为两片),养鸡场的一边靠着一面长为14m的墙,另几条边用总长为22m的竹篱笆围成,每片养鸡场的前面各开一个宽1m的门.求这个养鸡场的长与宽.

查看答案和解析>>
科目:初中数学 来源: 题型:
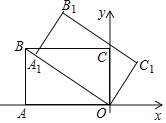
【题目】如图,平面直角坐标系中,矩形OABC的顶点A(﹣6,0),C(0,2![]() ).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.
).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种销售成本为每千克40元的水产品,据市场分析,若每千克50元销售,一个月能售出500kg,销售单价每涨2元,月销售量就减少20kg,针对这种水产品情况,请解答以下问题:
(1)当销售单价定为每千克55元时,计算销售量和月销售利润.
(2)商品想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A开始,沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动(点Q到达点C运动停止).如果点P,Q分别从点A,B同时出发t秒(t>0)
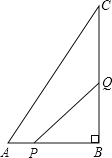
(1)t为何值时,PQ=6cm?
(2)t为何值时,可使得△PBQ的面积等于8cm2?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com