
【题目】阅读材料:
如图1,点![]() 是直线
是直线![]() 上一点,
上一点,![]() 上方的四边形
上方的四边形![]() 中,
中,![]() ,延长
,延长![]() ,
,![]() ,探究
,探究![]() 与
与![]() 的数量关系,并证明.
的数量关系,并证明.
小白的想法是:“作![]() (如图2),通过推理可以得到
(如图2),通过推理可以得到![]() ,从而得出结论”.
,从而得出结论”.
请按照小白的想法完成解答:
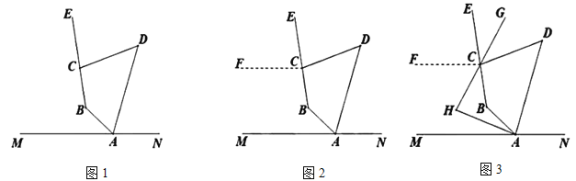
拓展延伸:
保留原题条件不变,![]() 平分
平分![]() ,反向延长
,反向延长![]() ,交
,交![]() 的平分线于点
的平分线于点![]() (如图3),设
(如图3),设![]() ,请直接写出
,请直接写出![]() 的度数(用含
的度数(用含![]() 的式子表示).
的式子表示).
【答案】阅读材料:![]() ,见解析;拓展延伸:
,见解析;拓展延伸:![]() .
.
【解析】
(1)作![]() ,
,![]() ,
,![]() ,由平行线性质可得
,由平行线性质可得![]() ,结合已知
,结合已知![]() ,可证
,可证![]() ,进而得到
,进而得到![]() ,从而
,从而![]() ,
,![]() ,将
,将![]() 代入可得
代入可得![]() .
.
(2)过H点作HP∥MN,可得∠CHA=∠PHA+∠PHC,结合(1)的结论和CG平分∠ECD可得∠PHC =∠FCH =120°-![]() ,即可得
,即可得![]() .
.
解:【阅读材料】
作![]() ,
,![]() ,
,![]() (如图1).
(如图1).
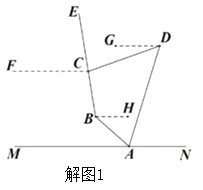
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]()
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() ,
,![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
【拓展延伸】
结论:![]() .
.
理由:如图,作![]() ,过H点作HP∥MN,
,过H点作HP∥MN,
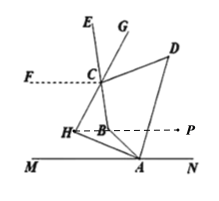
∴∠PHA=∠MAH=![]() ,
,
由(1)得FC∥MN,
∴FC∥HP,
∴∠PHC=∠FCH,
∵![]() ,CG平分∠ECD,
,CG平分∠ECD,
∴∠ECG=20°+![]() ,
,
∴∠FCH=![]()
=180°-(![]() )-(20°+
)-(20°+![]() )
)
=120°-![]()
∴∠CHA=∠PHA+∠PHC=![]() +(120°-
+(120°-![]() )=120°-
)=120°-![]()
即:![]() .
.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】课本拓展
旧知新意:
我们容易证明,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?
尝试探究

(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?
初步应用:
(2)如图2,在△ABC纸片中剪去△CED,得到四边形ABDE,∠1=130°,则∠2-∠C=______;
(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请利用上面的结论直接写出答案______.
3拓展提升:
(4)如图4,在四边形ABCD中,BP、CP分别平分外角∠EBC、∠FCB,∠P与∠A、∠D有何数量关系?为什么?(若需要利用上面的结论说明,可直接使用,不需要说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)如图所示,O是直线AB上一点,∠AOC=![]() ∠BOC,OC是∠AOD的平分线.
∠BOC,OC是∠AOD的平分线.

(1)求∠COD的度数.
(2)判断OD与AB的位置关系,并说出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产A,B两种产品共10件,其中A种产品的生产成本为每件3万元,B种产品的生产成本为每件5万元;并且销售一件A种产品的利润为1万元,销售一件B种产品的利润为2万元。
(1)若工厂计划获得总利润为14万元,问A,B两种产品应分别生产多少件?
(2)若工厂投入两种产品的总生产成本不多于44万元,且获得总利润多于14万元,问工厂有哪几种生产方案(即A,B两种产品各生产多少件)?
查看答案和解析>>
科目:初中数学 来源: 题型:
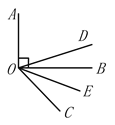
【题目】如图,DO平分∠AOC,OE平分∠BOC,若OA⊥OB,
(1)当∠BOC=30°,∠DOE=_______________; 当∠BOC=60°,∠DOE=_______________;
(2)通过上面的计算,猜想∠DOE的度数与∠AOB有什么关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)先完成下列表格:
a | …… | 0.0001 | 0.01 | 1 | 100 | 10000 | …… |
| …… | 0.01 | ______ | 1 | ______ | ______ | …… |
(2)由上表你发现什么规律?
(3)根据你发现的规律填空:
①已知![]() =1.732则
=1.732则![]() =______
=______![]() =______
=______
②已知![]() =0.056,则
=0.056,则![]() =______
=______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某房地产开发公司计划建 A,B 两种户型的住房 80 套,该公司所筹资金不 少于 2090 万元,但不超过 2096 万元,且所筹金全部用于建房,两种户型的建房成 本和售价如下表:

(1)该公司对两种户型的住房有哪几种建房方案?
(2)该公司选用哪种建房方案获得利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com