
【题目】某房地产开发公司计划建 A,B 两种户型的住房 80 套,该公司所筹资金不 少于 2090 万元,但不超过 2096 万元,且所筹金全部用于建房,两种户型的建房成 本和售价如下表:

(1)该公司对两种户型的住房有哪几种建房方案?
(2)该公司选用哪种建房方案获得利润最大?最大利润是多少?
【答案】有3种建房方案:①建A种户型48套,B种户型32套;②建A种户型49套,B种户型31套;③建A种户型50套,B种户型30套;(2)464万元.
【解析】
(1)设建A种户型x套,则B种户型(80-x)套,根据成本列出方程组进行求解;
(2)设利润为y,列出一次函数,根据函数的性质即可得到最大利润.
(1)设建A种户型x套,则B种户型(80-x)套,
依题意可得2090≤25x+28(80-x)≤2096
解得48≤x≤50
故有3种建房方案:①建A种户型48套,B种户型32套;②建A种户型49套,B种户型31套;③建A种户型50套,B种户型30套;
(2)设利润为y=(30-25)x+(35-28)(80-x)=-2x+560
∵y随x的增大而减小,
∴当x=48时,y最大值为-2×48+560=464万元.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:
如图1,点![]() 是直线
是直线![]() 上一点,
上一点,![]() 上方的四边形
上方的四边形![]() 中,
中,![]() ,延长
,延长![]() ,
,![]() ,探究
,探究![]() 与
与![]() 的数量关系,并证明.
的数量关系,并证明.
小白的想法是:“作![]() (如图2),通过推理可以得到
(如图2),通过推理可以得到![]() ,从而得出结论”.
,从而得出结论”.
请按照小白的想法完成解答:
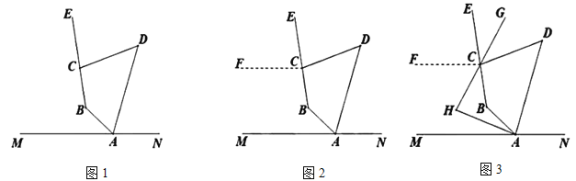
拓展延伸:
保留原题条件不变,![]() 平分
平分![]() ,反向延长
,反向延长![]() ,交
,交![]() 的平分线于点
的平分线于点![]() (如图3),设
(如图3),设![]() ,请直接写出
,请直接写出![]() 的度数(用含
的度数(用含![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在三角形ABC中,已知AC⊥BC,CD⊥AB,∠1=∠2.对于下列五个结论:
①DE∥AC;
②∠1=∠B;
③∠3=∠A;
④∠3=∠EDB;
⑤∠2与∠3互补.
其中正确的有( )

A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学组织学生春游,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满,已知45座客车每日每辆租金为220元,60座客车每日每辆租金为300元.试问:
(1)春游学生共多少人,原计划租45座客车多少辆?
(2)若租用同一种车,要使每位同学都有座位,怎样租车更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了调查同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取部分同学进行问卷测试,把测试成绩分成“优、良、中、差”四个等级,绘制了如下不完整的统计图:

根据以上统计信息,解答下列问题:
(1)求成绩是“优”的人数占抽取人数的百分比;
(2)求本次随机抽取问卷测试的人数;
(3)请把条形统计图补充完整;
(4)若该校学生人数为3000人,请估计成绩是“优”和“良”的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
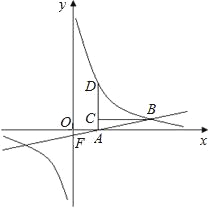
【题目】如图,点D在双曲线上,AD垂直x轴,垂足为A,点C在AD上,CB平行于x轴交双曲线于点B,直线AB与y轴交于点F,已知AC:AD=1:3,点C的坐标为(3,2).
(1)求该双曲线的解析式;
(2)求△OFA的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时间,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:

(1)图中自变量是______,因变量是______;
(2)小明家到学校的路程是 米;
(3)小明在书店停留了 分钟;
(4)本次上学途中,小明一共行驶了 米,一共用了 分钟;
(5)我们认为骑单车的速度超过300米/分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(-4,n)、B(3,4)是一次函数y1=kx+b的图象与反比例函数![]() 的图象的两个交点,过点D(t,0)(0<t<3)作x轴的垂线,分别交双曲线
的图象的两个交点,过点D(t,0)(0<t<3)作x轴的垂线,分别交双曲线![]() 和直线y1=kx+b于P、Q两点
和直线y1=kx+b于P、Q两点
(1) 直接写出反比例函数和一次函数的解析式
(2) 当t为何值时,S△BPQ=![]() S△APQ
S△APQ
(3) 以PQ为边在直线PQ的右侧作正方形PQMN,试说明:边QM与双曲线![]() (x>0)始终有交点
(x>0)始终有交点

查看答案和解析>>
科目:初中数学 来源: 题型:
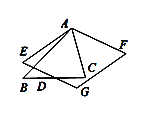
【题目】如图,△ABC中,∠BAC=60°,∠B=45°,AB=2,点D是BC上的一个动点,点D关于AB,AC的对称点分别是点E,F,四边形AEGF是平行四边形,则四边形AEGF面积的最小值是 ( )
A. 1B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com