
【题目】如图1,已知矩形AOCB,AB=6cm,BC=16cm,动点P从点A出发,以3cm/s的速度向点O运动,直到点O为止;动点Q同时从点C出发,以2cm/s的速度向点B运动,与点P同时结束运动.
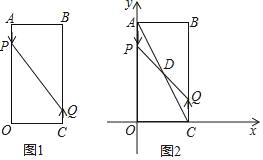
(1)当运动时间为2s时,P、Q两点的距离为 cm;
(2)请你计算出发多久时,点P和点Q之间的距离是10cm;
(3)如图2,以点O为坐标原点,OC所在直线为x轴,OA所在直线为y轴,1cm长为单位长度建立平面直角坐标系,连结AC,与PQ相交于点D,若双曲线![]() 过点D,问k的值是否会变化?若会变化,说明理由;若不会变化,请求出k的值.
过点D,问k的值是否会变化?若会变化,说明理由;若不会变化,请求出k的值.
【答案】(1)6![]() ;(2)t=
;(2)t=![]() 或t=
或t=![]() ,理由见解析;(3)k的值是不会变化,k=
,理由见解析;(3)k的值是不会变化,k= ![]() ,理由见解析
,理由见解析
【解析】
(1)构造出直角三角形,再求出PE,QE,利用勾股定理即可得出结论;
(2)同(2)的方法利用勾股定理建立方程求解即可得出结论;
(3)先求出直线AC解析式,再求出点P,Q坐标,进而求出直线PQ解析式,联立两解析式即可得出结论.
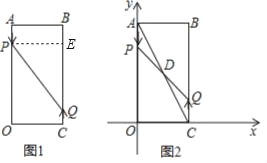
(1)如图1,由运动知,AP=3×2=6cm,CQ=2×2=4cm,
过点P作PE⊥BC于E,过点Q作QF⊥OA于F,
∴四边形APEB是矩形,
∴PE=AB=6,BE=6,
∴EQ=BC﹣BE﹣CQ=16﹣6﹣4=6,
根据勾股定理得,PQ=6![]() ,
,
故答案为6![]() ;
;
(2)设运动时间为t秒时,
由运动知,AP=3t,CQ=2t,
同(2)的方法得,PE=6,EQ=16﹣3t﹣2t=16﹣5t,
∵点P和点Q之间的距离是10cm,
∴62+(16﹣5t)2=100,
∴t=![]() 或t=
或t=![]() ;
;
(3)k的值是不会变化,
理由:∵四边形AOCB是矩形,
∴OC=AB=6,OA=16,
∴C(6,0),A(0,16),
设AC直线为y=kx+b,
把C(6,0),A(0,16)代入得![]() ,解得
,解得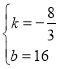
∴直线AC的解析式为y=﹣![]() x+16①,
x+16①,
设运动时间为t,
∴AP=3t,CQ=2t,
∴OP=16﹣3t,
∴P(0,16﹣3t),Q(6,2t),
设PQ直线为y=kx+b,
把P(0,16﹣3t),Q(6,2t),代入得![]() ,解得
,解得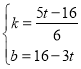
∴PQ解析式为y=![]() x+16﹣3t②,
x+16﹣3t②,
联立①②解得,x=![]() ,y=
,y=![]() ,
,
∴D(![]() ,
,![]() ),
),
∴k=![]() ×
×![]() =
=![]() 是定值.
是定值.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如果关于x的一元二次方程![]() 有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”.以下关于倍根方程的说法,正确的是________.(写出所有正确说法的序号).
有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”.以下关于倍根方程的说法,正确的是________.(写出所有正确说法的序号).
①方程![]() 是倍根方程;
是倍根方程;
②若![]() 是倍根方程,则
是倍根方程,则![]() ;
;
③若点![]() 在反比例函数
在反比例函数![]() 的图像上,则关于
的图像上,则关于![]() 的方程
的方程![]() 是倍根方程;
是倍根方程;
④若方程![]() 是倍根方程,且相异两点
是倍根方程,且相异两点![]() ,
, ![]() 都在抛物线
都在抛物线![]() 上,则方程
上,则方程![]() 的一个根为
的一个根为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=12,AB=10,则AE的长为( )

A.16 B.15 C.14 D.13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,D是BC中点,F是AC中点,AN是△ABC的外角∠MAC的角平分线,延长DF交AN于点E,连接CE.
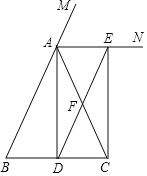
(1)求证:四边形ADCE是矩形;
(2)填空:①若BC=AB=4,则四边形ABDE的面积为 .
②当△ABC满足 时,四边形ADCE是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与函数y=![]() (x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=
(x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=![]() OC,且△ACD的面积是6,连接BC.
OC,且△ACD的面积是6,连接BC.
(1)求m,k,n的值;
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
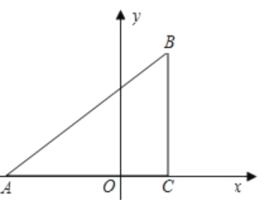
【题目】已知:如图,在平面直角坐标系中,![]() 是直角三角形,
是直角三角形,![]() ,点
,点![]() 的坐标分别为
的坐标分别为![]() ,
,![]()
(1)求过点![]() 的直线的函数表达式
的直线的函数表达式
(2)在![]() 轴上找一点
轴上找一点![]() ,连接
,连接![]() ,使得
,使得![]() 与
与![]() 相似(不包括全等),并求点
相似(不包括全等),并求点![]() 的坐标;
的坐标;
(3)在⑵的条件下,如![]() 分别是
分别是![]() 和
和![]() 上的动点,连接
上的动点,连接![]() ,设
,设![]() ,问是否存在这样的
,问是否存在这样的![]() 使得
使得![]() 与
与![]() 相似,如果存在,请求出
相似,如果存在,请求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C.过点C作CD∥x轴,交抛物线的对称轴于点D.
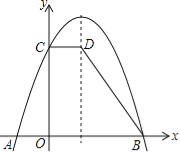
(1)求该抛物线的解析式;
(2)若将该抛物线向下平移m个单位,使其顶点落在D点,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com