
【题目】如图,△ABC中,AB=AC,D是BC中点,F是AC中点,AN是△ABC的外角∠MAC的角平分线,延长DF交AN于点E,连接CE.
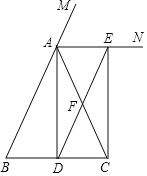
(1)求证:四边形ADCE是矩形;
(2)填空:①若BC=AB=4,则四边形ABDE的面积为 .
②当△ABC满足 时,四边形ADCE是正方形.
【答案】(1)见解析;(2)①4![]() ,②∠BAC=90°
,②∠BAC=90°
【解析】
(1)利用角平分线、等边对等角和外角可先证出∠MAE=∠B,所以AN∥BC,利用F是AC的中点可证△AFE≌△CFD,即可得到EF=FD,利用对角线互相平分的四边形是平行四边形所以四边形ADCE为平行四边形,再利用AB=AC,点D为BC中点,可以得到AD⊥BC,
有一个角是直角的平行四边形是矩形可得:四边形ADCE为矩形;
(2)由D、F分别是BC、AC的中点,利用中位线的性质可得:DF∥AB,易证四边形ABDE是平行四边形,利用BC=AB=4,AB=AC,可得△ABC是等边三角形,最后利用锐角三角函数求出高AD即可.
(3)可根据四边形ADCE是矩形,若再有一组邻边相等即为正方形不防使AD=DC,此时不难发现△ADC为等腰直角三角形,故∠ACB=45°,再根据△ABC为等腰三角形,即可得到∠BAC=90°.
证明:∵AN是△ABC外角∠CAM的平分线,
∴∠MAE=![]() ∠MAC,
∠MAC,
∵∠MAC=∠B+∠ACB,
∵AB=AC,
∴∠B=∠ACB,
∴∠MAE=∠B,
∴AN∥BC,
∴∠EAF=∠DCF
在△AFE和△CFD中

∴△AFE≌△CFD
∴EF=FD
∴四边形ADCE为平行四边形
∵AB=AC,点D为BC中点,
∴AD⊥BC,
∴∠ADC=90°,
∴四边形ADCE为矩形;
(2)①解:∵AB=AC,D是BC中点,F是AC中点,
∴DF∥AB,
由(1)知AE∥BD,
∴四边形ABDE是平行四边形,
∵BC=AB=4,AB=AC,
∴△ABC是等边三角形,
∴∠ABD=60°,
∵D为BC的中点,
∴∠ADC=90°,BD=2,
∴![]() ,
,
∴四边形ABDE的面积为BD×AD=2×![]() =4
=4![]() ,
,
故答案为:4![]() ;
;
②解:答案不唯一,如当∠BAC=90°时,四边形ADCE是正方形.
∵∠BAC=90°,AB=AC,
∴△ABC为等腰直角三角形,
∵D为BC的中点,
∴AD=DC,
∵四边形ADCE为矩形,
∴四边形ADCE为正方形.
故答案为:∠BAC=90°.


科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=10,BD=9,则△ADE的周长为( )
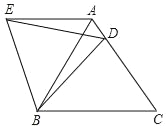
A. 19B. 20C. 27D. 30
查看答案和解析>>
科目:初中数学 来源: 题型:
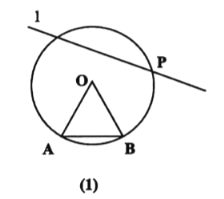
【题目】(一)如图(1),已知圆![]() ,点
,点![]() 、
、![]() 在圆上,且
在圆上,且![]() 为等边三角形,点
为等边三角形,点![]() 为直线
为直线![]() 与圆
与圆![]() 的一个交点.连接
的一个交点.连接![]() ,
,![]() ,证明:
,证明:![]()
(方法迁移)
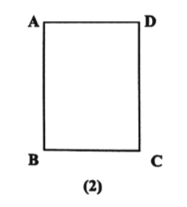
(二)如图(2),用直尺和圆规在矩形![]() 内作出所有的点
内作出所有的点![]() ,使得
,使得![]() (不写作法,保留作图痕迹).
(不写作法,保留作图痕迹).
(深入探究)
(三)已知矩形![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 边上的点,若满足
边上的点,若满足![]() 的点P恰有两个,求
的点P恰有两个,求![]() 的取值范围.
的取值范围.
(四)已知矩形![]() ,
,![]() ,
,![]() ,
,![]() 为矩形
为矩形![]() 内一点,且
内一点,且![]() ,若点
,若点![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 到点
到点![]() ,求
,求![]() 的最小值,并求此时
的最小值,并求此时![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有座抛物线形拱桥(如图),正常水位时桥下河面宽![]() ,河面距拱顶
,河面距拱顶![]() ,为了保证过往船只顺利航行,桥下水面的宽度不得小于
,为了保证过往船只顺利航行,桥下水面的宽度不得小于![]() .
.
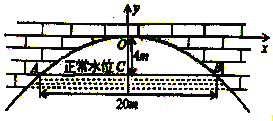
(1)求出如图所示坐标系中的抛物线的解析式;
(2)求水面在正常水位基础上上涨多少米时,就会影响过往船只航行?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝新中国成立70周年,河南省实验中学开展了以“我和我亲爱的祖国”为主题的“快闪”活动,九年级准备从两名男生和两名女生中选出两名同学领唱,如果每一位同学被选中的机会均等,则选出的恰为一位男生一位女生的概率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知矩形AOCB,AB=6cm,BC=16cm,动点P从点A出发,以3cm/s的速度向点O运动,直到点O为止;动点Q同时从点C出发,以2cm/s的速度向点B运动,与点P同时结束运动.
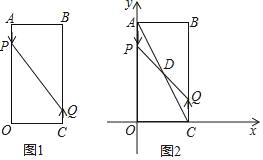
(1)当运动时间为2s时,P、Q两点的距离为 cm;
(2)请你计算出发多久时,点P和点Q之间的距离是10cm;
(3)如图2,以点O为坐标原点,OC所在直线为x轴,OA所在直线为y轴,1cm长为单位长度建立平面直角坐标系,连结AC,与PQ相交于点D,若双曲线![]() 过点D,问k的值是否会变化?若会变化,说明理由;若不会变化,请求出k的值.
过点D,问k的值是否会变化?若会变化,说明理由;若不会变化,请求出k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图1,二次函数y=ax2+2ax﹣3a(a≠0)图象的顶点为C与x轴交于A、B两点(点A在点B左侧),点C、B关于过点A的直线l:y=kx+![]() 对称.
对称.
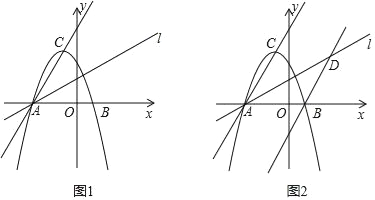
(1)求A、B两点坐标及直线l的解析式;
(2)求二次函数解析式;
(3)如图2,过点B作直线BD∥AC交直线l于D点,M、N分别为直线AC和直线l上的两个动点,连接CN,MM、MD,求CN+NM+MD的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示△ABC中,∠C=90°,∠A,∠B的平分线交于D点,DE⊥BC于点E,DF⊥AC于点F.
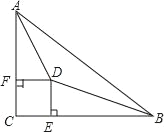
(1)求证:四边形CEDF为正方形;
(2)若AC=6,BC=8,求CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com