
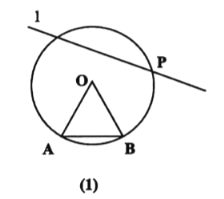
【题目】(一)如图(1),已知圆![]() ,点
,点![]() 、
、![]() 在圆上,且
在圆上,且![]() 为等边三角形,点
为等边三角形,点![]() 为直线
为直线![]() 与圆
与圆![]() 的一个交点.连接
的一个交点.连接![]() ,
,![]() ,证明:
,证明:![]()
(方法迁移)
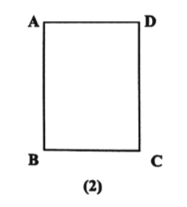
(二)如图(2),用直尺和圆规在矩形![]() 内作出所有的点
内作出所有的点![]() ,使得
,使得![]() (不写作法,保留作图痕迹).
(不写作法,保留作图痕迹).
(深入探究)
(三)已知矩形![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 边上的点,若满足
边上的点,若满足![]() 的点P恰有两个,求
的点P恰有两个,求![]() 的取值范围.
的取值范围.
(四)已知矩形![]() ,
,![]() ,
,![]() ,
,![]() 为矩形
为矩形![]() 内一点,且
内一点,且![]() ,若点
,若点![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 到点
到点![]() ,求
,求![]() 的最小值,并求此时
的最小值,并求此时![]() 的面积.
的面积.
【答案】(1)见详解;
(2)见详解 ;
(3)2![]() ≤m<2+
≤m<2+![]() .
.
(4)![]() 的最小值为
的最小值为![]() -2
-2![]() .,并求此时
.,并求此时![]() 的面积是
的面积是![]() .
.
【解析】
(1)根据圆周角定理即可证明;
(2)根据圆周角定理可知点∠BPC所对弧所对的圆心角等于90°,所以作出一个90°的圆心角即可;
(3)由点P要在AD上,且有两个,故AD应与圆O相交,且要在EF的上方,从而先算出临界值,则m在它们之间.
(4)先确定出当A,P,O在同一直线上时,AP取得最小值,从而得出此时PQ取得最小值,画出图形,利用勾股定理求解即可.利用相似三角形的性质和判定求出![]() 的高,再利用三角形的面积计算公式计算即可.
的高,再利用三角形的面积计算公式计算即可.
证明:(1)如图1所示,连接AP,BP.

∵![]() 为等边三角形,
为等边三角形,
∴∠AOB=60°.
∵∠APB=![]() ∠AOB,
∠AOB,
∴∠APB=30°.
解:(2)如图2所示:点P在![]() 上即可.
上即可.
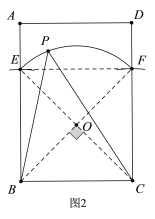
(3)由(2)得,要使![]() 的点P恰有两个,则AD与
的点P恰有两个,则AD与![]() 相交,如图3所示,
相交,如图3所示,
①当AD与⊙O相切时,连接OP,并延长PO与BC相交于Q,
∵AD与⊙O相切,
∴∠APQ=90°,
∵四边形ABCD是矩形,
∴∠A=∠ABQ=90°.
∴∠A=∠ABQ=∠APQ=90°.
∴四边形ABQP为矩形,
∴PQ=AB=m.
∵△BOC是等腰直角三角形,
∴OQ=![]() BC=
BC=![]() ,OB=2.
,OB=2.
∴PQ=2+![]() .
.
∴m<2+![]() .
.
②当AD与EF重合时,
m=BE=BC=2![]()
综上所述,m的取值范围为:2![]() ≤m<2+
≤m<2+![]() .
.
(4)如图4所示:
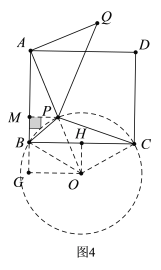
依题意可知,当A,P,O在同一直线上时,AP有最小值,此时PQ最小.
过点O作OH⊥BC于H,作OG⊥AB于G,过点P作PM⊥AB于M,连接OP,OB.
∵∠GBH=90°,
∴四边形BGOH为矩形,
∴OG=BH=![]() BC=
BC=![]() .
.
∵∠BPC=120°,
∴∠BOC=120°,
∵OB=OC,
∴∠OBH=30°.
∴设OH=x,则OB=2x.
在Rt△OBH中
OB2-OH2=BH2,
即4x2-x2=(![]() )2,
)2,
解得:x=1.
∴OH=1,OB=2.
∵AB=3,
∴AG=4.
在Rt△AGO中
OA=![]() =
=![]()
∴AP=![]() -2.
-2.
根据旋转的性质可知,AQ=AP=![]() -2,∠PAQ=90°,
-2,∠PAQ=90°,
根据勾股定理可求得:PQ=![]() =
=![]() AP=
AP=![]() -2
-2![]() .
.
∵OG⊥AB,PM⊥AB
∴PM∥OG,
∴![]() =
=![]()
∵OG=![]() ,AP=
,AP=![]() -2,OA=
-2,OA=![]()
∴PM=![]() .
.
∴![]() 的面积=
的面积=![]() AB
AB![]() PM=
PM=![]() 3
3![]() =
=![]() .
.
答:![]() 的最小值为
的最小值为![]() -2
-2![]() .,并求此时
.,并求此时![]() 的面积是
的面积是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有若干个除颜色外其余均相同的红、黄、蓝三种颜色的小球,其中红球2个,蓝球1个,若从中任意摸出一个球,摸到的球是红球的概率为![]() .
.
(1)求袋中黄球的个数;
(2)第一次任意摸出一个球(不放回),第二次再摸出一个球,利用树状图或刘表格求两次摸到球的颜色是红色与黄色的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在Rt△ABC 中, ![]() ,D、E是斜边BC上两动点,且∠DAE=45°,将△
,D、E是斜边BC上两动点,且∠DAE=45°,将△![]() 绕点
绕点![]() 逆时针旋转90后,得到△
逆时针旋转90后,得到△![]() ,连接
,连接![]() .
.
(1)试说明:△![]() ≌△
≌△![]() ;
;
(2)当BE=3,CE=9时,求∠BCF的度数和DE的长;
(3)如图2,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,D是斜边BC所在直线上一点,BD=3,BC=8,求DE2的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
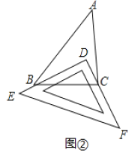
【题目】材料阅读:如图①所示的图形,像我们常见的学习用品—圆规.我们不妨把这样图形叫做“规形图”.
解决问题:

(1)观察“规形图”,试探究![]() 与
与![]() ,
,![]() ,
,![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(2)请你直接利用以上结论,解决以下两个问题:
Ⅰ.如图②,把一块三角尺![]() 放置在
放置在![]() 上,使三角尺的两条直角边
上,使三角尺的两条直角边![]() ,
,![]() 恰好经过点
恰好经过点![]() ,
,![]() ,若
,若![]() ,则
,则![]() _____
_____![]() .
.
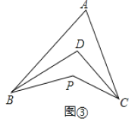
Ⅱ.如图③,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx+m(k<0)与抛物线y=x2+bx+c相交于抛物线的顶点P和另一点Q.
(1)若点P(2,﹣c),Q的横坐标为﹣1.求点Q的坐标;
(2)过点Q作x轴的平行线与抛物线y=x2+bx+c的对称轴相交于点E,直线PQ与y轴交于点M,若PE=2EQ,c=![]() (﹣
(﹣![]() ≤b<﹣2),求点Q的纵坐标;
≤b<﹣2),求点Q的纵坐标;
(3)在(2)的条件下,求△OMQ的面积S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.
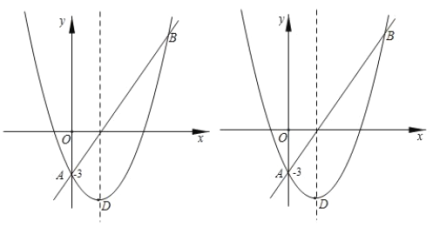
(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,D是BC中点,F是AC中点,AN是△ABC的外角∠MAC的角平分线,延长DF交AN于点E,连接CE.
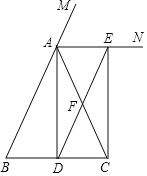
(1)求证:四边形ADCE是矩形;
(2)填空:①若BC=AB=4,则四边形ABDE的面积为 .
②当△ABC满足 时,四边形ADCE是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《朗读者》自播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,沭阳县某中学开展“朗读”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示。
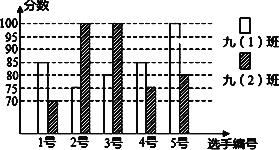
⑴根据图示填写表格;
平均数 | 中位数 | 众数 | |
九⑴班 | 85 | 85 | |
九⑵班 | 80 |
⑵如果规定成绩较稳定的班级胜出,你认为哪个班级能胜出?说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com