
【题目】在一个不透明的口袋里装有若干个除颜色外其余均相同的红、黄、蓝三种颜色的小球,其中红球2个,蓝球1个,若从中任意摸出一个球,摸到的球是红球的概率为![]() .
.
(1)求袋中黄球的个数;
(2)第一次任意摸出一个球(不放回),第二次再摸出一个球,利用树状图或刘表格求两次摸到球的颜色是红色与黄色的概率.
【答案】(1)1个;(2) ![]() .
.
【解析】
(1)首先设袋中的黄球个数为x个,然后根据古典概率的知识列方程,求解即可求得答案;
(2)首先画表格,然后求得全部情况的总数与符合条件的情况数目,求其二者的比值即可.
.解:(1)设袋中的黄球个数为![]() 个,由题意得
个,由题意得![]()
解得:![]()
∴袋中黄球的个数1个.
(2)这是随机事件中的等可能事件,列表如下:
第一次 第二次 | 红1 | 红2 | 黄 | 监 |
红1 | (红1,红2) | (红1.黄) | (红1,蓝) | |
红2 | (红2,红1) | (红2,黄) | (红2,蓝) | |
黄 | (黄,红1) | (黄,红2) | (黄,蓝) | |
蓝 | (蓝,红1) | (蓝,红2) | (蓝,黄) |
由表可知,共有12神等可能的結果,其中両次摸到球的顔色是紅色与黄色的有4种:(红1,黄),(红2,黄),(黄,红1),(黄,红2),
所以两次摸到球的颜色是红色与黄色的概率为:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】一商品销售某种商品,平均每天可售出20件,每件盈利50元.为了扩大销售,增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.
(1)若每件商品降价2元,则平均每天可售出______件;
(2)当每件商品降价多少元时,该商品每天的销售利润为1600元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】辰星旅游度假村有甲种风格客房15间,乙种风格客房20间.按现有定价:若全部入住,一天营业额为8500元;若甲、乙两种风格客房均有10间入住,一天营业额为5000元.
(1)求甲、乙两种客房每间现有定价分别是多少元?
(2)度假村以乙种风格客房为例,市场情况调研发现:若每个房间每天按现有定价,房间会全部住满;当每个房间每天的定价每增加20元时,就会有两个房间空闲.如果游客居住房间,度假村需对每个房间每天支出80元的各种费用.当每间房间定价为多少元时,乙种风格客房每天的利润![]() 最大,最大利润是多少元?
最大,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形![]() 中,
中,![]() ,点
,点![]() ,
,![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() ,
,![]() 上,且
上,且![]() 垂直
垂直![]() .
.
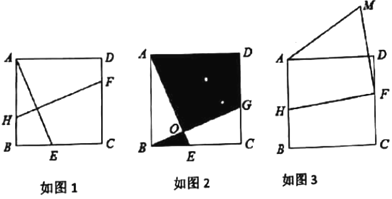
(1)如图1,求证:![]() ;
;
(2)如图2,平移线段![]() 至线段
至线段![]() ,
,![]() 交
交![]() 于点
于点![]() ,图中阴影部分的面积与正方形的面积之比为
,图中阴影部分的面积与正方形的面积之比为![]() ,求
,求![]() 的周长;
的周长;
(3)如图3,若![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 至线段
至线段![]() ,连接
,连接![]() ,则线段
,则线段![]() 的最小值为______.
的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于半径为
中,对于半径为![]() 的
的![]() 和点
和点![]() ,给出如下定义:
,给出如下定义:
若![]() ,则称
,则称![]() 为
为![]() 的“近外点”.
的“近外点”.
(1)当![]() 的半径为2时,点
的半径为2时,点![]() ,
,![]() ,
,![]() ,
,![]() 中,
中,![]() 的“近外点”是__________;
的“近外点”是__________;
(2)若点![]() 是
是![]() 的“近外点”,求
的“近外点”,求![]() 的半径
的半径![]() 的取值范围;
的取值范围;
(3)当![]() 的半径为2时,直线
的半径为2时,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若线段
,若线段![]() 上存在
上存在![]() 的“近外点”,直接写出
的“近外点”,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ΔABC中,∠BAC=120°,AB=AC=6cm,点M从点A出发沿AB方向以每秒一个单位长的速度向点B匀速运动,与此同时点N也从点A出发沿AC方向以相同的速度向点C匀速运动,过点N作DN∥AB,交BC于点D,连接MD,设运动的时间是t秒(![]() ).
).
(1)填空:![]() ____________;
____________;
(2)是否存在某一时刻,使得四边形MBDN的面积与三角形ABC的面积比为4:9,若存在求![]() 值,若不存在请说明理由;
值,若不存在请说明理由;
(3)当![]() 为何值时,ΔMND为等腰三角形?请直接写出符合条件的
为何值时,ΔMND为等腰三角形?请直接写出符合条件的![]() 值.
值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标是(1,3),将点A绕原点O顺时针旋转90°得到点A′,则点A′的坐标是( )
A. (-3,1) B. (3,-1) C. (-1,3) D. (1,-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=10,BD=9,则△ADE的周长为( )
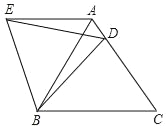
A. 19B. 20C. 27D. 30
查看答案和解析>>
科目:初中数学 来源: 题型:
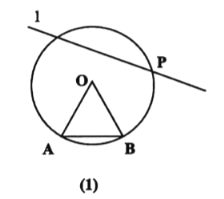
【题目】(一)如图(1),已知圆![]() ,点
,点![]() 、
、![]() 在圆上,且
在圆上,且![]() 为等边三角形,点
为等边三角形,点![]() 为直线
为直线![]() 与圆
与圆![]() 的一个交点.连接
的一个交点.连接![]() ,
,![]() ,证明:
,证明:![]()
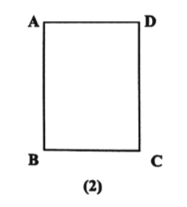
(方法迁移)
(二)如图(2),用直尺和圆规在矩形![]() 内作出所有的点
内作出所有的点![]() ,使得
,使得![]() (不写作法,保留作图痕迹).
(不写作法,保留作图痕迹).
(深入探究)
(三)已知矩形![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 边上的点,若满足
边上的点,若满足![]() 的点P恰有两个,求
的点P恰有两个,求![]() 的取值范围.
的取值范围.
(四)已知矩形![]() ,
,![]() ,
,![]() ,
,![]() 为矩形
为矩形![]() 内一点,且
内一点,且![]() ,若点
,若点![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 到点
到点![]() ,求
,求![]() 的最小值,并求此时
的最小值,并求此时![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com