
【题目】在正方形![]() 中,
中,![]() ,点
,点![]() ,
,![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() ,
,![]() 上,且
上,且![]() 垂直
垂直![]() .
.
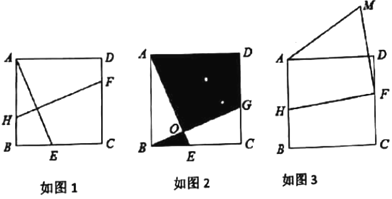
(1)如图1,求证:![]() ;
;
(2)如图2,平移线段![]() 至线段
至线段![]() ,
,![]() 交
交![]() 于点
于点![]() ,图中阴影部分的面积与正方形的面积之比为
,图中阴影部分的面积与正方形的面积之比为![]() ,求
,求![]() 的周长;
的周长;
(3)如图3,若![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 至线段
至线段![]() ,连接
,连接![]() ,则线段
,则线段![]() 的最小值为______.
的最小值为______.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,利用直角三角形两锐角互余的关系可得
,利用直角三角形两锐角互余的关系可得![]() ,利用ASA可证明
,利用ASA可证明![]() ,根据全等三角形的性质即可得结论;(2)根据阴影部分的面积与正方形
,根据全等三角形的性质即可得结论;(2)根据阴影部分的面积与正方形![]() 的面积之比为
的面积之比为![]() 可求出空白部分的面积,根据
可求出空白部分的面积,根据![]() 可求出△ABO的面积,设
可求出△ABO的面积,设![]() ,
,![]() ,可得ab=4,根据勾股定理可得a2+b2=16,即可求出a+b=
,可得ab=4,根据勾股定理可得a2+b2=16,即可求出a+b=![]() ,进而可求出△ABO的周长;(3)过点
,进而可求出△ABO的周长;(3)过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() ,过B作BP//HF,交CD于P,可证明四边形
,过B作BP//HF,交CD于P,可证明四边形![]() 是平行四边形,可得
是平行四边形,可得![]() ,设
,设![]() ,分别用a表示出CN和CF的长,根据勾股定理表示出NF的长,利用二次函数的性质求出最小值即可.
,分别用a表示出CN和CF的长,根据勾股定理表示出NF的长,利用二次函数的性质求出最小值即可.
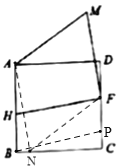
(1)如图,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,
∵四边形ABCD是正方形,点![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 上,
上,
∴BH//GF,![]() ,
,![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
∵![]() 垂直
垂直![]() ,HF//BG,
,HF//BG,
∴![]() 垂直
垂直![]() ,
,
∴![]() ,
,
∵∠ABE=![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,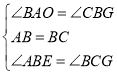 ,
,
∴![]() ,
,
∴![]() ,
,
∴AE=HF.
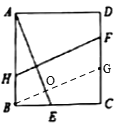
(2)∵阴影部分的面积与正方形![]() 的面积之比为
的面积之比为![]() ,
,
∴阴影部分的面积为![]() ,
,
∴空白部分的面积为![]() ,
,
由(1)得,![]() ,
,
∴![]() 的面积与四边形
的面积与四边形![]() 的面积相等,
的面积相等,
∴S△AOB=![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,即
,即![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() 的周长=AB+OA+OB=
的周长=AB+OA+OB=![]() .
.
(3)过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() ,过B作BP//HF,交CD于P,
,过B作BP//HF,交CD于P,
∵![]() ,
,
∴![]() ,
,
由(1)得![]() ,△ABN≌△BCP,BH=PF,
,△ABN≌△BCP,BH=PF,
∴BN=CP,
∵![]() ,
,
∴![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
设![]() ,则
,则![]() ,CP=4-2a,
,CP=4-2a,
∴![]() ,
,
∴CN=4-BN=2a,
∴![]()
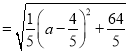 ,
,
∴当![]() 时,
时,![]() 取得最小值
取得最小值![]() .
.


科目:初中数学 来源: 题型:
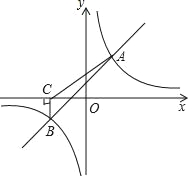
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(2,3),B(﹣3,n)两点.
的图象交于A(2,3),B(﹣3,n)两点.
(1)求一次函数与反比例函数的解析式;
(2)过点B作BC⊥x轴,垂足为C,连接AC,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学课上,张老师出示了一个题目:“如图,ABCD的对角线相交于点O,过点O作EF垂直于BD交AB,CD分别于点F,E,连接DF,![]() 请根据上述条件,写出一个正确结论
请根据上述条件,写出一个正确结论![]() ”其中四位同学写出的结论如下:
”其中四位同学写出的结论如下:
小青:![]() ;小何:四边形DFBE是正方形;
;小何:四边形DFBE是正方形;
小夏:![]() ;小雨:
;小雨:![]() .
.
这四位同学写出的结论中不正确的是![]()
![]()

A. 小青 B. 小何 C. 小夏 D. 小雨
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段![]() 的最小覆盖圆就是以线段
的最小覆盖圆就是以线段![]() 为直径的圆.
为直径的圆.
(1)请分别作出图①中两个三角形的最小覆盖圆(要求用尺规作图,保留作图痕迹,不写作法);
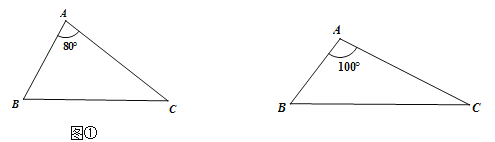
(2)三角形的最小覆盖圆有何规律?请直接写出你所得到的结论(不要求证明);
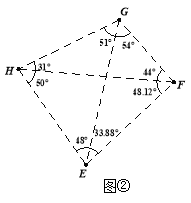
(3)某城市有四个小区![]() (其位置如图②所示),现拟建一个手机信号基站,为了使这四个小区居民的手机都能有信号,且使基站所需发射功率最小(距离越小,所需功率越小),此基站应建在何处?请写出你的结论并说明研究思路.
(其位置如图②所示),现拟建一个手机信号基站,为了使这四个小区居民的手机都能有信号,且使基站所需发射功率最小(距离越小,所需功率越小),此基站应建在何处?请写出你的结论并说明研究思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有若干个除颜色外其余均相同的红、黄、蓝三种颜色的小球,其中红球2个,蓝球1个,若从中任意摸出一个球,摸到的球是红球的概率为![]() .
.
(1)求袋中黄球的个数;
(2)第一次任意摸出一个球(不放回),第二次再摸出一个球,利用树状图或刘表格求两次摸到球的颜色是红色与黄色的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。
相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。

(1)求抛物线的解析式;
(2)在(1)中抛物线的第二象限图象上是否存在一点P,使△POB与△POC全等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料阅读:如图①所示的图形,像我们常见的学习用品—圆规.我们不妨把这样图形叫做“规形图”.
解决问题:

(1)观察“规形图”,试探究![]() 与
与![]() ,
,![]() ,
,![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(2)请你直接利用以上结论,解决以下两个问题:
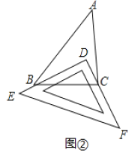
Ⅰ.如图②,把一块三角尺![]() 放置在
放置在![]() 上,使三角尺的两条直角边
上,使三角尺的两条直角边![]() ,
,![]() 恰好经过点
恰好经过点![]() ,
,![]() ,若
,若![]() ,则
,则![]() _____
_____![]() .
.
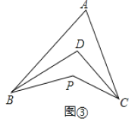
Ⅱ.如图③,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com