
【题目】我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段![]() 的最小覆盖圆就是以线段
的最小覆盖圆就是以线段![]() 为直径的圆.
为直径的圆.
(1)请分别作出图①中两个三角形的最小覆盖圆(要求用尺规作图,保留作图痕迹,不写作法);
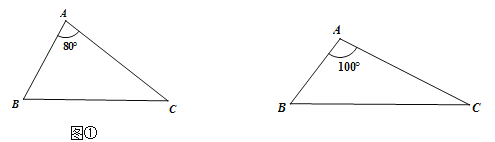
(2)三角形的最小覆盖圆有何规律?请直接写出你所得到的结论(不要求证明);
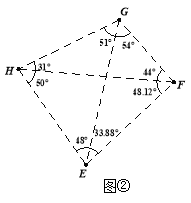
(3)某城市有四个小区![]() (其位置如图②所示),现拟建一个手机信号基站,为了使这四个小区居民的手机都能有信号,且使基站所需发射功率最小(距离越小,所需功率越小),此基站应建在何处?请写出你的结论并说明研究思路.
(其位置如图②所示),现拟建一个手机信号基站,为了使这四个小区居民的手机都能有信号,且使基站所需发射功率最小(距离越小,所需功率越小),此基站应建在何处?请写出你的结论并说明研究思路.
【答案】(1)图形见解析;(2)锐角三角形的最小覆盖圆是其外接圆,钝角三角形的最小覆盖圆是以其最长边为直径的圆,直角三角形的最小覆盖圆二者均可.(3)![]() 的外接圆的圆心为手机信号基站所在位置.
的外接圆的圆心为手机信号基站所在位置.
【解析】
试题分析:(1)画出△ABC的外接圆即可;(2)锐角三角形的最小覆盖圆是其外接圆,钝角三角形的最小覆盖圆是以其最长边为直径的圆,直角三角形的最小覆盖圆二者均可.(3)![]() 的外接圆的圆心为手机信号基站所在位置.
的外接圆的圆心为手机信号基站所在位置.
试题解析:(1)如图所示:
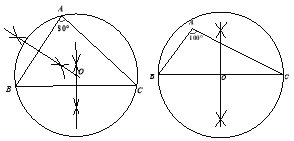
(2)锐角三角形的最小覆盖圆是其外接圆,钝角三角形的最小覆盖圆是以其最长边为直径的圆,直角三角形的最小覆盖圆二者均可.
(说明:写出三角形的最小覆盖圆是其外接圆,或是以其最长边为直径的圆,各给1分)
(3)结论:![]() 的外接圆的圆心为手机信号基站所在位置.
的外接圆的圆心为手机信号基站所在位置.
研究思路:
a.手机信号基站应建在四边形![]() 的最小覆盖圆的圆心处;所以先考虑四边形
的最小覆盖圆的圆心处;所以先考虑四边形![]() 的外接圆,因为对角不互补,所以该四边形没有外接圆;
的外接圆,因为对角不互补,所以该四边形没有外接圆;
b.作四边形对角线,将四边形分割成两个三角形,考虑其中一个三角形的最小覆盖圆能否覆盖另一个三角形,从而将四边形最小覆盖圆问题转化为三角形最小覆盖圆问题来研究;
c.若沿![]() 分割,因为
分割,因为![]() ,所以这两个三角形的最小覆盖圆均不能完全覆盖另一个三角形;
,所以这两个三角形的最小覆盖圆均不能完全覆盖另一个三角形;
d.若沿![]() 分割,因为
分割,因为![]() ,所以存在一个三角形的最小覆盖圆能完全覆盖另一个三角形的情况,又因为
,所以存在一个三角形的最小覆盖圆能完全覆盖另一个三角形的情况,又因为![]() ,所以
,所以![]() 的最小覆盖圆,即其外接圆能完全覆盖
的最小覆盖圆,即其外接圆能完全覆盖![]() ,因此
,因此![]() 的外接圆的圆心为手机信号基站所在位置.
的外接圆的圆心为手机信号基站所在位置.
(说明:1.学生的答案只要涉及到将四边形问题转化为三角形问题,可以给第6分;
2.若学生答案含有以下情况之一,并借此分析沿![]() 分割和沿
分割和沿![]() 分割的差异性,均可以给第7分:
分割的差异性,均可以给第7分:
①比较四边形对角和的数量关系;
②同弧所对的圆周角的度数关系;
③画出四个三角形的最小覆盖圆,通过观察或测量,比较大小后发现![]() 的外接圆的圆心为手机信号站
的外接圆的圆心为手机信号站
所在位置.
3.重在判断学生思维的方向,不过多的要求语言的规范和思维的严谨.)


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,交BC于点E(BE>EC),且BD=2![]() .过点D作DF∥BC,交AB的延长线于点F.
.过点D作DF∥BC,交AB的延长线于点F.
(1)求证:DF为⊙O的切线;
(2)若∠BAC=60°,DE=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+(m+2)x+2m-1=0.
(1)求证方程有两个不相等的实数根.
(2)当m为何值时,方程的两根互为相反数?并求出此时方程的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,四边形
中,四边形![]() 为正方形,点
为正方形,点![]() 的坐标为
的坐标为![]() ,动点
,动点![]() 沿边
沿边![]() 从
从![]() 向
向![]() 以每秒
以每秒![]() 的速度运动,同时动点
的速度运动,同时动点![]() 沿边
沿边![]() 从
从![]() 向
向![]() 以同样的速度运动,连接
以同样的速度运动,连接![]() 、
、![]() 交于点
交于点![]() .
.
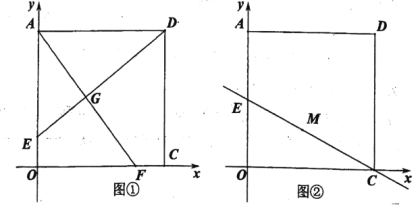
(1)试探索线段![]() 、
、![]() 的关系,写出你的结论并说明理由;
的关系,写出你的结论并说明理由;
(2)连接![]() 、
、![]() ,分别取
,分别取![]() 、
、![]() 、
、![]() 、
、![]() 的中点
的中点![]() 、
、![]() 、
、![]() 、
、![]() ,则四边形
,则四边形![]() 是什么特殊平行四边形?请在图①中补全图形,并说明理由.
是什么特殊平行四边形?请在图①中补全图形,并说明理由.
(3)如图②当点![]() 运动到
运动到![]() 中点时,点
中点时,点![]() 是直线
是直线![]() 上任意一点,点
上任意一点,点![]() 是平面内任意一点,是否存在点
是平面内任意一点,是否存在点![]() 使以
使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,请直接写出点
为顶点的四边形是菱形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形![]() 中,
中,![]() ,点
,点![]() ,
,![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() ,
,![]() 上,且
上,且![]() 垂直
垂直![]() .
.
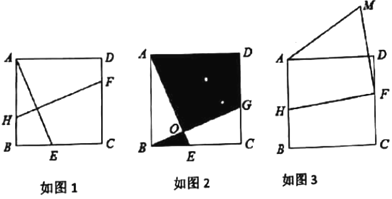
(1)如图1,求证:![]() ;
;
(2)如图2,平移线段![]() 至线段
至线段![]() ,
,![]() 交
交![]() 于点
于点![]() ,图中阴影部分的面积与正方形的面积之比为
,图中阴影部分的面积与正方形的面积之比为![]() ,求
,求![]() 的周长;
的周长;
(3)如图3,若![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 至线段
至线段![]() ,连接
,连接![]() ,则线段
,则线段![]() 的最小值为______.
的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图的折线统计图,则符合这一结果的实验最有可能的是( )

A.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
C.暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球
D.掷一个质地均匀的正六面体骰子,向上的面点数是4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ΔABC中,∠BAC=120°,AB=AC=6cm,点M从点A出发沿AB方向以每秒一个单位长的速度向点B匀速运动,与此同时点N也从点A出发沿AC方向以相同的速度向点C匀速运动,过点N作DN∥AB,交BC于点D,连接MD,设运动的时间是t秒(![]() ).
).
(1)填空:![]() ____________;
____________;
(2)是否存在某一时刻,使得四边形MBDN的面积与三角形ABC的面积比为4:9,若存在求![]() 值,若不存在请说明理由;
值,若不存在请说明理由;
(3)当![]() 为何值时,ΔMND为等腰三角形?请直接写出符合条件的
为何值时,ΔMND为等腰三角形?请直接写出符合条件的![]() 值.
值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图象如图所示,图象过点
的部分图象如图所示,图象过点![]() ,对称轴为直线
,对称轴为直线![]() ,
,
下列结论:
①![]() ;
;
②![]() ;
;
③![]() ;
;
④若点![]() ,点
,点![]() ,点
,点![]() 在该函数图象上,则
在该函数图象上,则![]() ;
;
⑤若方程![]() 的两根为
的两根为![]() 和
和![]() ,且
,且![]() ,则
,则![]() .
.
其中正确的结论有( )
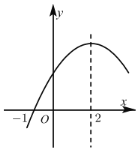
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长方形OABC绕顶点C(0,5)逆时针方向旋转,当旋转到CO′A′B′位置时,边O′A′交边AB于D,且A′D=2,AD=4.
(1)求BC长;
(2)求阴影部分的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com