
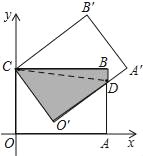
【题目】长方形OABC绕顶点C(0,5)逆时针方向旋转,当旋转到CO′A′B′位置时,边O′A′交边AB于D,且A′D=2,AD=4.
(1)求BC长;
(2)求阴影部分的面积.

【答案】(1)7;(2)16.
【解析】
(1)根据旋转的特性得出BC=AO=O′A′,AB=CO=CO'=5,∠B=∠O'=90°,之后利用勾股定理根据题意建立方程求解即可
(2)将不规则的阴影部分分解成由两个三角形组成,之后分别求出两个方程面积相加即可
解:(1)∵长方形OABC绕顶点C(0,5)逆时针方向旋转得到矩形CO′A′B′
∴BC=AO=O′A′,AB=CO=CO'=5,∠B=∠O'=90°,
∵AD=4,AB=5,
∴BD=5﹣4=1,
设BC=x,则DO'=O'A'﹣A'D=x﹣2,
连接CD,则BC2+BD2=CD2=CO'2+DO'2
即x2+12=52+(x﹣2)2
解得:x=7,
∴BC=7;
(2)∵BC=7,BD=1,CO'=5,DO'=7﹣2=5,∠B=∠O'=90°,
∴阴影部分的面积=△BCD面积+△O'CD面积=![]() ×7×1+
×7×1+![]() ×5×5=16.
×5×5=16.


科目:初中数学 来源: 题型:
【题目】我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段![]() 的最小覆盖圆就是以线段
的最小覆盖圆就是以线段![]() 为直径的圆.
为直径的圆.
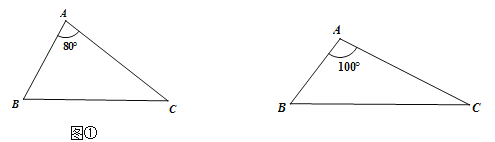
(1)请分别作出图①中两个三角形的最小覆盖圆(要求用尺规作图,保留作图痕迹,不写作法);
(2)三角形的最小覆盖圆有何规律?请直接写出你所得到的结论(不要求证明);
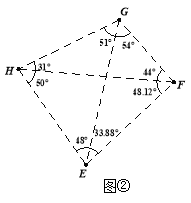
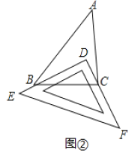
(3)某城市有四个小区![]() (其位置如图②所示),现拟建一个手机信号基站,为了使这四个小区居民的手机都能有信号,且使基站所需发射功率最小(距离越小,所需功率越小),此基站应建在何处?请写出你的结论并说明研究思路.
(其位置如图②所示),现拟建一个手机信号基站,为了使这四个小区居民的手机都能有信号,且使基站所需发射功率最小(距离越小,所需功率越小),此基站应建在何处?请写出你的结论并说明研究思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的一元二次方程![]() 有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”.以下关于倍根方程的说法,正确的是________.(写出所有正确说法的序号).
有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”.以下关于倍根方程的说法,正确的是________.(写出所有正确说法的序号).
①方程![]() 是倍根方程;
是倍根方程;
②若![]() 是倍根方程,则
是倍根方程,则![]() ;
;
③若点![]() 在反比例函数
在反比例函数![]() 的图像上,则关于
的图像上,则关于![]() 的方程
的方程![]() 是倍根方程;
是倍根方程;
④若方程![]() 是倍根方程,且相异两点
是倍根方程,且相异两点![]() ,
, ![]() 都在抛物线
都在抛物线![]() 上,则方程
上,则方程![]() 的一个根为
的一个根为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
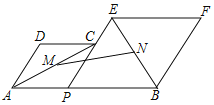
【题目】如图,已知AB=12,P为线段AB上的一个动点,分别以AP、PB为边在AB的同侧作菱形APCD和菱形PBFE,点P、C、E在一条直线上,∠DAP=60°.M、N分别是对角线AC、BE的中点.当点P在线段AB上移动时,点M、N之间的距离最短为______.(结果留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料阅读:如图①所示的图形,像我们常见的学习用品—圆规.我们不妨把这样图形叫做“规形图”.
解决问题:

(1)观察“规形图”,试探究![]() 与
与![]() ,
,![]() ,
,![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(2)请你直接利用以上结论,解决以下两个问题:
Ⅰ.如图②,把一块三角尺![]() 放置在
放置在![]() 上,使三角尺的两条直角边
上,使三角尺的两条直角边![]() ,
,![]() 恰好经过点
恰好经过点![]() ,
,![]() ,若
,若![]() ,则
,则![]() _____
_____![]() .
.
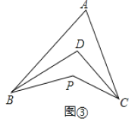
Ⅱ.如图③,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售某种商品,每件成本为30元.经市场调研,售价为40元时,每月可销售200件;售价每涨1元,每月销售量将减少10件.该商场每月要在这种商品上盈利2160元的同时.尽可能的减少库存,那么这种商品售价应该定为多少元?
(1)解:方法1:设这种商品的定价为![]() 元,由题意,得方程为: ;
元,由题意,得方程为: ;
方法2:设这种商品涨了![]() 元,由题意,得方程为: ;
元,由题意,得方程为: ;
(2)请你选择一种方法,写出完整的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=12,AB=10,则AE的长为( )

A.16 B.15 C.14 D.13
查看答案和解析>>
科目:初中数学 来源: 题型:
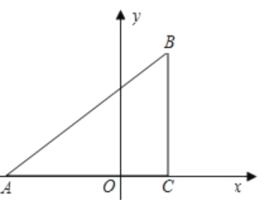
【题目】已知:如图,在平面直角坐标系中,![]() 是直角三角形,
是直角三角形,![]() ,点
,点![]() 的坐标分别为
的坐标分别为![]() ,
,![]()
(1)求过点![]() 的直线的函数表达式
的直线的函数表达式
(2)在![]() 轴上找一点
轴上找一点![]() ,连接
,连接![]() ,使得
,使得![]() 与
与![]() 相似(不包括全等),并求点
相似(不包括全等),并求点![]() 的坐标;
的坐标;
(3)在⑵的条件下,如![]() 分别是
分别是![]() 和
和![]() 上的动点,连接
上的动点,连接![]() ,设
,设![]() ,问是否存在这样的
,问是否存在这样的![]() 使得
使得![]() 与
与![]() 相似,如果存在,请求出
相似,如果存在,请求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com