
【题目】如图,△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,交BC于点E(BE>EC),且BD=2![]() .过点D作DF∥BC,交AB的延长线于点F.
.过点D作DF∥BC,交AB的延长线于点F.
(1)求证:DF为⊙O的切线;
(2)若∠BAC=60°,DE=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.

【答案】(1)详见解析;(2)9![]() ﹣2π.
﹣2π.
【解析】
(1)连结OD,根据垂径定理得到OD⊥BC,根据平行线的性质得到OD⊥DF,根据切线的判定定理证明;
(2)连结OB,连结OD交BC于P,作BH⊥DF于H,证明△OBD为等边三角形,得到∠ODB=60°,OB=BD=2![]() ,根据勾股定理求出PE,证明△ABE∽△AFD,根据相似三角形的性质求出AE,根据阴影部分的面积=△BDF的面积-弓形BD的面积计算.
,根据勾股定理求出PE,证明△ABE∽△AFD,根据相似三角形的性质求出AE,根据阴影部分的面积=△BDF的面积-弓形BD的面积计算.
证明:(1)连结OD,
∵AD平分∠BAC交⊙O于D,
∴∠BAD=∠CAD,
∴![]() ,
,
∴OD⊥BC,
∵BC∥DF,
∴OD⊥DF,
∴DF为⊙O的切线;
(2)连结OB,连结OD交BC于P,作BH⊥DF于H,
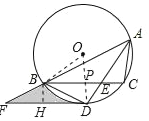
∵∠BAC=60°,AD平分∠BAC,
∴∠BAD=30°,
∴∠BOD=2∠BAD=60°,
∴△OBD为等边三角形,
∴∠ODB=60°,OB=BD=2![]() ,
,
∴∠BDF=30°,
∵BC∥DF,
∴∠DBP=30°,
在Rt△DBP中,PD=![]() BD=
BD=![]() ,PB=
,PB=![]() PD=3,
PD=3,
在Rt△DEP中,∵PD=![]() ,DE=
,DE=![]() ,
,
∴PE=![]() =2,
=2,
∵OP⊥BC,
∴BP=CP=3,
∴CE=3﹣2=1,
∵∠DBE=∠CAE,∠BED=∠AEC,
∴△BDE∽△ACE,
∴AE:BE=CE:DE,即AE:5=1:![]() ,
,
∴AE=![]()
∵BE∥DF,
∴△ABE∽△AFD,
∴![]() ,即
,即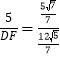 ,
,
解得DF=12,
在Rt△BDH中,BH=![]() BD=
BD=![]() ,
,
∴阴影部分的面积=△BDF的面积﹣弓形BD的面积=△BDF的面积﹣(扇形BOD的面积﹣△BOD的面积)=![]() =9
=9![]() ﹣2π.
﹣2π.


科目:初中数学 来源: 题型:
【题目】校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道![]() 上确定点D,使CD与
上确定点D,使CD与![]() 垂直,测得CD的长等于21米,在
垂直,测得CD的长等于21米,在![]() 上点D的同侧取点A、B,使∠CAD=300,∠CBD=600.
上点D的同侧取点A、B,使∠CAD=300,∠CBD=600.
(1)求AB的长(精确到0.1米,参考数据:![]() );
);
(2)已知本路段对校车限速为40千米/小时,若测得某辆校车从A到B用时2秒,这辆校车是否超速?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=![]() 与x轴、y轴分别交于A、B两点,P是以C(0,2)为圆心,2为半径的圆上一动点,连结PA、PB.则△PAB面积的最小值是_____.
与x轴、y轴分别交于A、B两点,P是以C(0,2)为圆心,2为半径的圆上一动点,连结PA、PB.则△PAB面积的最小值是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
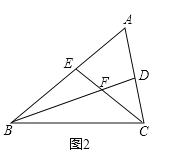
【题目】已知:如图(1)所示,在△ABC中,BD平分∠ABC , CD平分∠ACB,过D点作EF∥BC,与AB交于点E,与AC交于点F
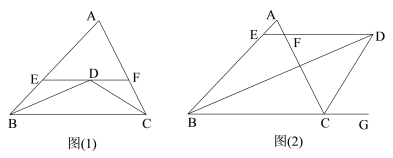
(1)若BE=3,CF=2,求EF的长;
(2)如图(2)所示,若∠ABC的平分线BD与△ABC的外角∠ACG的平分线CD相交于点D,其它条件不变,请写出EF,BE,CF之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的两条角平分线,且
的两条角平分线,且![]() ,
,![]() 交于点
交于点![]() .
.
(1)如图1,用等式表示![]() ,
,![]() ,
,![]() 这三条线段之间的数量关系,并证明你的结论;
这三条线段之间的数量关系,并证明你的结论;
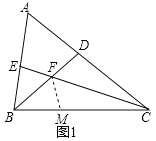
小东通过观察、实验,提出猜想:![]() .他发现先在
.他发现先在![]() 上截取
上截取![]() ,使
,使![]() ,连接
,连接![]() ,再利用三角形全等的判定和性质证明
,再利用三角形全等的判定和性质证明![]() 即可.
即可.
①下面是小东证明该猜想的部分思路,请补充完整:
ⅰ)在![]() 上截取
上截取![]() ,使
,使![]() ,连接
,连接![]() ,则可以证明
,则可以证明![]() 与 全等,判定它们全等的依据是 ;
与 全等,判定它们全等的依据是 ;
ⅱ)由![]() ,
,![]() ,
,![]() 是
是![]() 的两条角平分线,可以得出
的两条角平分线,可以得出![]() °;
°;
②请直接利用ⅰ),ⅱ)已得到的结论,完成证明猜想![]() 的过程.
的过程.
(2)如图2,若![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的袋子中有四张标有数字1,2,3,4的卡片,小明、小华两人按照各自的规则玩抽卡片游戏。
小明画出树形图如下:

小华列出表格如下:
第一次 第二次 | 1 | 2 | 3 | 4 |
1 | (1,1) | (2,1) | (3,1) | (4,1) |
2 | (1,2) | (2,2) | ① | (4,2) |
3 | (1,3) | (2,3) | (3,3) | (4,3) |
4 | (1,4) | (2,4) | (3,4) | (4,4) |
回答下列问题:
(1)根据小明画出的树形图分析,他的游戏规则是:随机抽出一张卡片后 (填“放回”或“不放回”),再随机抽出一张卡片;
(2)根据小华的游戏规则,表格中①表示的有序数对为 ;
(3)规定两次抽到的数字之和为奇数的获胜,你认为淮获胜的可能性大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
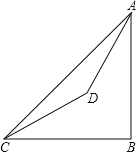
【题目】已知:如图,在山脚的![]() 处测得山顶
处测得山顶![]() 的仰角为
的仰角为![]() ,沿着坡度为
,沿着坡度为![]() 的斜坡前进
的斜坡前进![]() 米到
米到![]() 处(即
处(即![]() ,
,![]() 米),测得
米),测得![]() 的仰角为
的仰角为![]() ,求此山的高度
,求此山的高度![]() .(答案保留根号)
.(答案保留根号)
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com