
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的两条角平分线,且
的两条角平分线,且![]() ,
,![]() 交于点
交于点![]() .
.
(1)如图1,用等式表示![]() ,
,![]() ,
,![]() 这三条线段之间的数量关系,并证明你的结论;
这三条线段之间的数量关系,并证明你的结论;
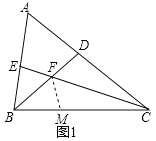
小东通过观察、实验,提出猜想:![]() .他发现先在
.他发现先在![]() 上截取
上截取![]() ,使
,使![]() ,连接
,连接![]() ,再利用三角形全等的判定和性质证明
,再利用三角形全等的判定和性质证明![]() 即可.
即可.
①下面是小东证明该猜想的部分思路,请补充完整:
ⅰ)在![]() 上截取
上截取![]() ,使
,使![]() ,连接
,连接![]() ,则可以证明
,则可以证明![]() 与 全等,判定它们全等的依据是 ;
与 全等,判定它们全等的依据是 ;
ⅱ)由![]() ,
,![]() ,
,![]() 是
是![]() 的两条角平分线,可以得出
的两条角平分线,可以得出![]() °;
°;
②请直接利用ⅰ),ⅱ)已得到的结论,完成证明猜想![]() 的过程.
的过程.
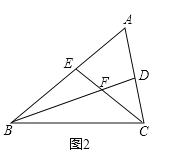
(2)如图2,若![]() ,求证:
,求证:![]() .
.
【答案】(1)①ⅰ)△BMF,边角边;ⅱ)60;②详见解析;(2)详见解析
【解析】
(1)先得出结论;
①利用三角形内角和求出∠ABC+∠ACB=120°,进而得出∠FBC+∠FCB=60°,得出∠BFC=120°,即可得出结论;
②利用角平分线得出∠EBF=∠MBF,进而得出△BEF≌△BMF,求出∠BFM,即可判断出∠CFM=∠CFD,即可判断出△FCM≌△FCD,即可得出结论;
(2)先求出相关角的度数,进而判断出BG=CE,进而判断出△BGF≌△CEA,即可得出结论.
(1)![]()
①如图1,在![]() 上取一点
上取一点![]() ,使
,使![]() ,
,
ⅰ)![]() 是
是![]() 的平分线,
的平分线,
![]() ,
,
在![]() 和
和![]() 中,
中,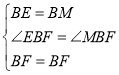 ,
,
![]() ;
;
ⅱ)![]() ,
,![]() 是
是![]() 的两条角平分线,
的两条角平分线,
![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
故答案为:ⅰ)ΔBMF,SAS;ⅱ)60;
②由①知,![]() ,
,![]() ,
,
![]() ,
,
∵![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是
是![]() 的平分线,
的平分线,
![]() ,
,
在![]() 和
和![]() 中,
中,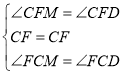
![]() ,
,
![]() ,
,
![]() ;
;
(2)如图2,在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() 是
是![]() 的两条角平分线,
的两条角平分线,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 的边
的边![]() 左侧作
左侧作![]() ,交
,交![]() 的延长线于
的延长线于![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,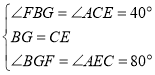 ,
,
![]() ,
,
![]() .
.


 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
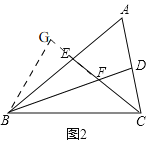
【题目】如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.
(1)求证:BD=EC;
(2)若AB=5, BD=6时,求△ACE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F连接AE、DE、DF.
(1)证明:∠E=∠C;
(2)若∠E=58°,求∠BDF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,交BC于点E(BE>EC),且BD=2![]() .过点D作DF∥BC,交AB的延长线于点F.
.过点D作DF∥BC,交AB的延长线于点F.
(1)求证:DF为⊙O的切线;
(2)若∠BAC=60°,DE=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,A(0,3),B(4,0),C(﹣1,﹣1),点 P 线段 AB上一动点,将线段 AB 绕原点 O 旋转一周,点 P 的对应点为 P′,则 P′C 的最大值为_____,最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
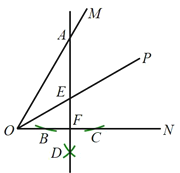
【题目】如图,![]() 平分
平分![]() ,
,![]() 是边
是边![]() 上一点,以点
上一点,以点![]() 为圆心,大于点
为圆心,大于点![]() 到
到![]() 的距离为半径作弧,交
的距离为半径作弧,交![]() 于点
于点![]() 、
、![]() ,再分别以点
,再分别以点![]() 、
、![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧交于点
的长为半径作弧,两弧交于点![]() ,作直线
,作直线![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,若
,若![]() ,
,![]() ,则
,则![]() __________.
__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
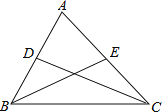
【题目】如图,已知![]() 中,延长
中,延长![]() 边上的中线
边上的中线![]() 到
到![]() ,使
,使![]() ,延长
,延长![]() 边上的中线
边上的中线![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() .
.
(1)补全图形;
(2)![]() 的大小关系如何?证明你的结论;
的大小关系如何?证明你的结论;
(3)![]() 三点的位置关系如何?证明你的结论.
三点的位置关系如何?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°、AD是角平分线,E为AC边上的点,DE=DB,下列结论:①∠DEA+∠B=180°;② ∠CDE=∠CAB;③ AC=![]() (AB+AE);④ S△ADC=
(AB+AE);④ S△ADC=![]() S四边形ABDE,其中正确的结论个数为( )
S四边形ABDE,其中正确的结论个数为( )
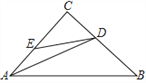
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com