
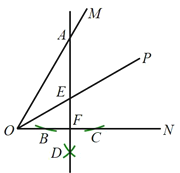
【题目】如图,![]() 平分
平分![]() ,
,![]() 是边
是边![]() 上一点,以点
上一点,以点![]() 为圆心,大于点
为圆心,大于点![]() 到
到![]() 的距离为半径作弧,交
的距离为半径作弧,交![]() 于点
于点![]() 、
、![]() ,再分别以点
,再分别以点![]() 、
、![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧交于点
的长为半径作弧,两弧交于点![]() ,作直线
,作直线![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,若
,若![]() ,
,![]() ,则
,则![]() __________.
__________.
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AC=BC,AC的垂直平分线分别交AC,BC于点E,F.点D为AB边的中点,点M为EF上一动点,若AB=4,△ABC的面积是16,则△ADM周长的最小值为( )
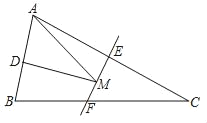
A.20B.16C.12D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的两条角平分线,且
的两条角平分线,且![]() ,
,![]() 交于点
交于点![]() .
.
(1)如图1,用等式表示![]() ,
,![]() ,
,![]() 这三条线段之间的数量关系,并证明你的结论;
这三条线段之间的数量关系,并证明你的结论;
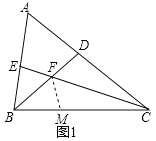
小东通过观察、实验,提出猜想:![]() .他发现先在
.他发现先在![]() 上截取
上截取![]() ,使
,使![]() ,连接
,连接![]() ,再利用三角形全等的判定和性质证明
,再利用三角形全等的判定和性质证明![]() 即可.
即可.
①下面是小东证明该猜想的部分思路,请补充完整:
ⅰ)在![]() 上截取
上截取![]() ,使
,使![]() ,连接
,连接![]() ,则可以证明
,则可以证明![]() 与 全等,判定它们全等的依据是 ;
与 全等,判定它们全等的依据是 ;
ⅱ)由![]() ,
,![]() ,
,![]() 是
是![]() 的两条角平分线,可以得出
的两条角平分线,可以得出![]() °;
°;
②请直接利用ⅰ),ⅱ)已得到的结论,完成证明猜想![]() 的过程.
的过程.
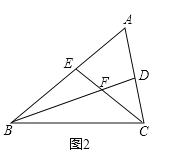
(2)如图2,若![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形 ABCD 中,M 是 BC 边上一点,且点 M 不与 B、C 重合,点 P 在射线 AM 上,将线段 AP 绕点 A 顺时针旋转 90°得到线段 AQ,连接BP,DQ.
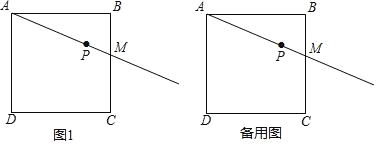
(1)依题意补全图 1;
(2)①连接 DP,若点 P,Q,D 恰好在同一条直线上,求证:DP2+DQ2=2AB2;
②若点 P,Q,C 恰好在同一条直线上,则 BP 与 AB 的数量关系为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的袋子中有四张标有数字1,2,3,4的卡片,小明、小华两人按照各自的规则玩抽卡片游戏。
小明画出树形图如下:

小华列出表格如下:
第一次 第二次 | 1 | 2 | 3 | 4 |
1 | (1,1) | (2,1) | (3,1) | (4,1) |
2 | (1,2) | (2,2) | ① | (4,2) |
3 | (1,3) | (2,3) | (3,3) | (4,3) |
4 | (1,4) | (2,4) | (3,4) | (4,4) |
回答下列问题:
(1)根据小明画出的树形图分析,他的游戏规则是:随机抽出一张卡片后 (填“放回”或“不放回”),再随机抽出一张卡片;
(2)根据小华的游戏规则,表格中①表示的有序数对为 ;
(3)规定两次抽到的数字之和为奇数的获胜,你认为淮获胜的可能性大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线![]() 的一部分.请根据图中信息解答下列问题:
的一部分.请根据图中信息解答下列问题:

(1)恒温系统在这天保持大棚内温度18℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,已知抛物线 L1:y=﹣x2+2x+3 与 x 轴交于 A,B 两点(点 A在点 B 的左侧),与 y 轴交于点 C,在 L1 上任取一点 P,过点 P 作直线 l⊥x 轴, 垂足为D,将 L1 沿直线 l 翻折得到抛物线L2,交 x 轴于点 M,N(点 M 在点 N 的左侧).
(1)当 L1 与 L2 重合时,求点 P 的坐标;
(2)当点 P 与点 B 重合时,求此时 L2 的解析式;并直接写出 L1 与 L2 中,y 均随x 的增大而减小时的 x 的取值范围;
(3)连接 PM,PB,设点 P(m,n),当 n=![]() m 时,求△PMB 的面积.
m 时,求△PMB 的面积.
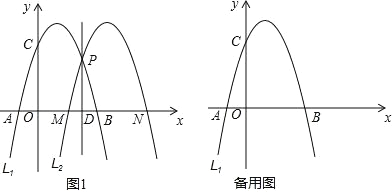
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com