
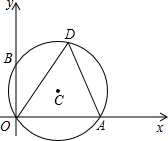
 如图,⊙C经过坐标原点O,点B的坐标是(0,2),∠ODA=60°.
如图,⊙C经过坐标原点O,点B的坐标是(0,2),∠ODA=60°.分析 (1)连接AB,根据圆周角定理得到AB为⊙C的直径和∠ABO=∠ODA=60°,根据直角三角形的性质求出OA的长,得到答案;
(2)根据直角三角形的性质求出⊙C的半径,根据三角形的面积公式计算即可.
解答 解:(1)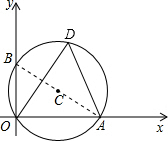 连接AB,
连接AB,
∵∠AOB=90°,
∴AB为⊙C的直径,
∵∠ABO=∠ODA=60°,
∴OAB=30°,
∴OA=2$\sqrt{3}$,
∴点A的坐标(2$\sqrt{3}$,0);
(2)∵OAB=30°,OB=2,
∴AB=4,
∴⊙C的面积=π×22=4π.
点评 本题考查的是圆周角定理的应用、坐标与图形的关系,掌握同弧所对的圆周角相等、90°的圆周角所对的弦是直径是解题的关键.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
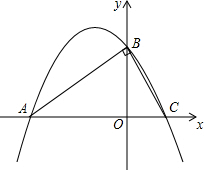 在△ABC中,∠ABC=90°,点C在x轴正半轴上,点A在x轴负半轴上,点B在y轴正半轴上如图所示,若tan∠BAC=$\frac{1}{2}$,OB=2,求经过A、B、C点的抛物线的解析式.
在△ABC中,∠ABC=90°,点C在x轴正半轴上,点A在x轴负半轴上,点B在y轴正半轴上如图所示,若tan∠BAC=$\frac{1}{2}$,OB=2,求经过A、B、C点的抛物线的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 家电名称 | 电饭煲 | 洗衣机 | 热水器 |
| 使用时间段 | 8:00~8:20 | 21:05~21:45 | 20:45~21:20 |
| 用电量/kW•h | 0.4 | 0.6 | 3.5 |
| 电费/元 | 0.22 | 0.18 | 1.425 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
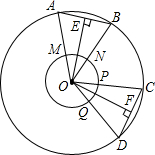 如图所示.两个同心圆⊙O,点A、B、C、D在外圆上,点M、N、P、Q在内圆上,0E是AB的弦心距,OF平分∠COD,且$\widehat{MN}$=$\widehat{PQ}$,求证:OE=OF.
如图所示.两个同心圆⊙O,点A、B、C、D在外圆上,点M、N、P、Q在内圆上,0E是AB的弦心距,OF平分∠COD,且$\widehat{MN}$=$\widehat{PQ}$,求证:OE=OF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com