
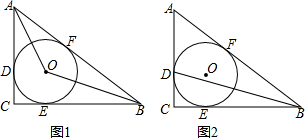
分析 (1)如图1,连接DO、EO、FO,利用切线的定义和性质可得∠DOE=90°,AF=AD,BF=BE,易得△ADO≌△AFO,由全等三角形的性质可得∠AOF=∠AOD,∠BOF=∠BOE,易得$∠AOB=\frac{1}{2}(360°-∠DOE)$;
(2)过点D作DM⊥AB于点M,如图2,由tan∠DBC=$\frac{1}{4}$,可知$\frac{CD}{CB}=\frac{1}{4}$,设DC=1,则BC=4,可得CE=CD=1,BF=BE=3,设AD=AF=x,易得AC、AB,由勾股定理可得x,由△ADM∽△ABC,利用相似三角形的性质可得$\frac{AD}{AB}=\frac{AM}{AC}=\frac{DM}{BC}$,易得AM,DM,BM,由tan∠ADB=$\frac{DM}{BM}$可得结果.
解答 解:(1)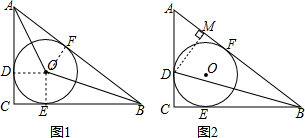 如图1,连接DO、EO、FO,
如图1,连接DO、EO、FO,
∵AC、BC、AB均为⊙O的切线,
∴AF=AD,BF=BE,CE=CD,∠∠ODC=90°,∠OEC=90°,
∵∠C=90°,
∴∠DOE=90°,
在△ADO与△AFO中,
$\left\{\begin{array}{l}{AF=AD}\\{∠AFO=∠ADO=90°}\\{FO=DO}\end{array}\right.$,
∴△ADO≌△AFO,
∴∠AOF=∠AOD,
同理可得,∠BOF=∠BOE,
∴$∠AOB=∠AOD+∠BOE=\frac{1}{2}×$(360°-90°)=135°;
(2)过点D作DM⊥AB于点M,如图2,
∵tan$∠DBC=\frac{CD}{CB}=\frac{1}{4}$,
∴设DC=1,则BC=4,
∴CE=CD=1,BF=BE=3,
设AD=AF=x,则AC=1+x,AB=3+x,
在Rt△ABC中,(x+1)2+42=(x+3)2,
解得:x=2,
∵△ADM∽△ABC,
∴$\frac{AD}{AB}=\frac{AM}{AC}=\frac{DM}{BC}$,
∴$\frac{2}{5}=\frac{AM}{3}=\frac{DM}{4}$,
∴AM=$\frac{6}{5}$,DM=$\frac{8}{5}$,∴$BM=5-\frac{6}{5}$=$\frac{19}{5}$,
∴tan∠ABD=$\frac{DM}{BM}=\frac{\frac{8}{5}}{\frac{19}{5}}$=$\frac{8}{19}$.
点评 此题主要考查了切线的性质,作出恰当的辅助线,构建直角三角形是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 36×104 | B. | 3.6×104 | C. | 0.36×105 | D. | 3.6×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点A的坐标是(2,0),△ABO是等边三角形,点B在第一象限,若反比例函数y=$\frac{k}{x}$的图象经过点B,则k的值是$\sqrt{3}$.
如图,点A的坐标是(2,0),△ABO是等边三角形,点B在第一象限,若反比例函数y=$\frac{k}{x}$的图象经过点B,则k的值是$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
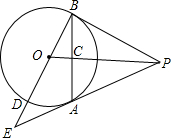 如图,PA为⊙O的切线,A为切点,过A作OP的垂线AB,垂足为点C,交⊙O于点B.延长BO与⊙O交于点B,延长BO与⊙O交于点D,与PA的延长线交于点E,
如图,PA为⊙O的切线,A为切点,过A作OP的垂线AB,垂足为点C,交⊙O于点B.延长BO与⊙O交于点B,延长BO与⊙O交于点D,与PA的延长线交于点E,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
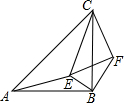 如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.
如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 全体实数 | B. | 全体整数 | ||
| C. | n≥3 | D. | 大于或等于3的整数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com