
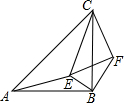
 如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.
如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.分析 (1)首先由△ABC和△CEF均为等腰直角三角形可得AC:BC=CE:CF,∠ACE=∠BCF;然后根据相似三角形判定的方法,推得△CAE∽△CBF即可;
(2)首先根据△CAE∽△CBF,判断出∠CAE=∠△CBF,再根据∠CAE+∠CBE=90°,判断出∠EBF=90°;然后在Rt△BEF中,根据勾股定理,求出EF的长度,再根据CE、EF的关系,求出CE的长是多少即可.
解答 (1)证明:∵△ABC和△CEF均为等腰直角三角形,
∴$\frac{AC}{BC}$=$\frac{CE}{CF}$=$\sqrt{2}$,
∴∠ACB=∠ECF=45°,
∴∠ACE=∠BCF,
∴△CAE∽△CBF;
(2)解:∵△CAE∽△CBF,
∴∠CAE=∠CBF,$\frac{AE}{BF}$=$\frac{AC}{BC}$=$\sqrt{2}$,
又∵$\frac{AE}{BF}$=$\frac{AC}{BC}$=$\sqrt{2}$,AE=2
∴$\frac{2}{BF}$=$\sqrt{2}$,∴BF=$\sqrt{2}$,
又∵∠CAE+∠CBE=90°,
∴∠CBF+∠CBE=90°,
∴∠EBF=90°,
∴EF2=BE2+BF2=12+($\sqrt{2}$)2=3,
∴EF=$\sqrt{3}$,
∵CE2=2EF2=6,
∴CE=$\sqrt{6}$.
点评 此题考查相似三角形的判定和性质,正方形的性质,掌握相似三角形的判定方法是解决问题的前提.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
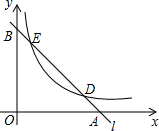 已知直线l分别与x轴、y轴交于A、B两点,与双曲线y=$\frac{m}{x}$(m≠0,x>0)分别交于D、E两点,若点D的坐标为(4,1),点E的坐标为(1,n)
已知直线l分别与x轴、y轴交于A、B两点,与双曲线y=$\frac{m}{x}$(m≠0,x>0)分别交于D、E两点,若点D的坐标为(4,1),点E的坐标为(1,n)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
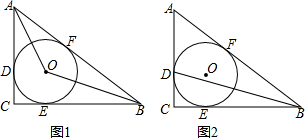
 如图,已知矩形ABCD的四个顶点位于双曲线y=$\frac{k}{x}$上,且点A的横坐标为$\frac{\sqrt{5}-1}{2}$,S矩形ABCD=2$\sqrt{5}$,则k=1.
如图,已知矩形ABCD的四个顶点位于双曲线y=$\frac{k}{x}$上,且点A的横坐标为$\frac{\sqrt{5}-1}{2}$,S矩形ABCD=2$\sqrt{5}$,则k=1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
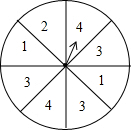 如图,一个可以自由转动的圆形转盘,转盘分成8个大小相同的扇形,上面分别标有数字1、2、3、4,指针的位置固定,转动的转盘停止后,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形).转动转盘一次,当转盘停止转动时,则指针指向标有“3”所在区域的概率为$\frac{3}{8}$.
如图,一个可以自由转动的圆形转盘,转盘分成8个大小相同的扇形,上面分别标有数字1、2、3、4,指针的位置固定,转动的转盘停止后,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形).转动转盘一次,当转盘停止转动时,则指针指向标有“3”所在区域的概率为$\frac{3}{8}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com