
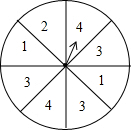
 如图,一个可以自由转动的圆形转盘,转盘分成8个大小相同的扇形,上面分别标有数字1、2、3、4,指针的位置固定,转动的转盘停止后,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形).转动转盘一次,当转盘停止转动时,则指针指向标有“3”所在区域的概率为$\frac{3}{8}$.
如图,一个可以自由转动的圆形转盘,转盘分成8个大小相同的扇形,上面分别标有数字1、2、3、4,指针的位置固定,转动的转盘停止后,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形).转动转盘一次,当转盘停止转动时,则指针指向标有“3”所在区域的概率为$\frac{3}{8}$.  应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:选择题
 墨墨对他所住小区的100户居民2月份天然气的使用量(单位:m3)进行统计,其结果如图所示,图中36-38段因不小心洒上水而看不清,则2月份天然气的使用量在36-38段的居民有( )
墨墨对他所住小区的100户居民2月份天然气的使用量(单位:m3)进行统计,其结果如图所示,图中36-38段因不小心洒上水而看不清,则2月份天然气的使用量在36-38段的居民有( )| A. | 18户 | B. | 20户 | C. | 22户 | D. | 24户 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点A的坐标是(2,0),△ABO是等边三角形,点B在第一象限,若反比例函数y=$\frac{k}{x}$的图象经过点B,则k的值是$\sqrt{3}$.
如图,点A的坐标是(2,0),△ABO是等边三角形,点B在第一象限,若反比例函数y=$\frac{k}{x}$的图象经过点B,则k的值是$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
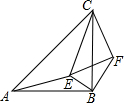 如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.
如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com