
分析 作DH⊥BC于H,根据三角形中位线定理求出AD、BC,根据勾股定理计算即可.
解答 解: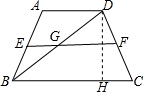 作DH⊥BC于H,
作DH⊥BC于H,
∵EF是梯形ABCD的中位线,
∴EG、GF分别是△ABD和△DBC的中位线,
∴AD=2EG=8厘米,BC=2GF=20厘米,
∴CH=(20-8)÷2=6厘米,BH=14厘米,
∴DH=$\sqrt{C{D}^{2}-C{H}^{2}}=6\sqrt{3}$厘米,
∴BD=$\sqrt{B{H}^{2}+D{H}^{2}}$=4$\sqrt{19}$厘米,
故答案为:4$\sqrt{19}$.
点评 本题考查的是梯形的中位线定理和等腰梯形的性质的应用,掌握三角形的中位线定理、梯形的中位线定理是解题的关键,注意勾股定理的应用.


 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:初中数学 来源: 题型:解答题
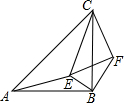 如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.
如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 全体实数 | B. | 全体整数 | ||
| C. | n≥3 | D. | 大于或等于3的整数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
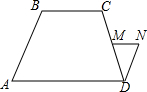 如图,在梯形ABCD中,AD∥BC,M是CD中点,MN∥AD,DN∥AB,设BC=a,AD=b(a<b),那么MN与a、b有怎样的数量关系.试加以证明.
如图,在梯形ABCD中,AD∥BC,M是CD中点,MN∥AD,DN∥AB,设BC=a,AD=b(a<b),那么MN与a、b有怎样的数量关系.试加以证明.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②④ | C. | ③④⑤ | D. | ②④⑤ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com