
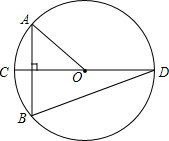
 如图,⊙O的直径CD垂直于弦AB,∠AOC=40°,则∠CDB的度数为( )
如图,⊙O的直径CD垂直于弦AB,∠AOC=40°,则∠CDB的度数为( )| A. | 40° | B. | 30° | C. | 20° | D. | 10° |
科目:初中数学 来源: 题型:解答题
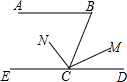 如图,已知AB∥CD,CN是∠BCE的平分线.
如图,已知AB∥CD,CN是∠BCE的平分线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
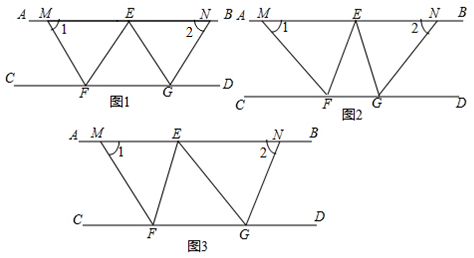
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
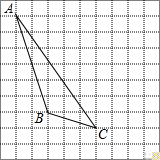 如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.
如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 墨墨对他所住小区的100户居民2月份天然气的使用量(单位:m3)进行统计,其结果如图所示,图中36-38段因不小心洒上水而看不清,则2月份天然气的使用量在36-38段的居民有( )
墨墨对他所住小区的100户居民2月份天然气的使用量(单位:m3)进行统计,其结果如图所示,图中36-38段因不小心洒上水而看不清,则2月份天然气的使用量在36-38段的居民有( )| A. | 18户 | B. | 20户 | C. | 22户 | D. | 24户 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
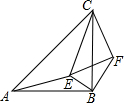 如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.
如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com