
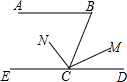
 如图,已知AB∥CD,CN是∠BCE的平分线.
如图,已知AB∥CD,CN是∠BCE的平分线.分析 (1)利用角平分线的定义和补角的定义可得结果;
(2)由垂直的定义可得∠MCN=90°,即∠BCN+∠BCM=90°,利用等式的性质可得2∠BCN+2∠BCM=180°,又因为∠BCE=2∠BCN,可得∠BCD=2∠BCM,即得结论;
(3)延长AB至F,过N,M分别作NG∥AB,MH∥AB,则有NG∥AB∥MH∥CD,利用平行线的性质易得∠BNG=∠ABN,∠CNG=∠ECN,∠BMH=∠FBM,∠CMH=∠DCM,由∠MBN=∠MCN=90°,可得∠ABN+∠FBM+∠ECN+∠DCM=180°,由角平分线的定义可得结论.
解答 (1)解:∵CN、CM分别平分∠BCE和∠BCD,
∴$∠BCN=\frac{1}{2}∠BCE$,$∠BCM=\frac{1}{2}∠BCD$,
∵∠BCE+∠BCD=180°,
∴∠MCN=∠BCN+∠BCM=$\frac{1}{2}∠BCE+∠BCD$=$\frac{1}{2}$(∠BCE+∠BCD)=90°;
(2)证明:∵CM⊥CN,
∴∠MCN=90°,
即∠BCN+∠BCM=90°,
∴2∠BCN+2∠BCM=180°,
∵CN是∠BCE的平分线,
∴∠BCE=2∠BCN,
∴∠BCE+2∠BCM=180°,
∴∠BCD=2∠BCM,
∴CM平分∠BCD;
(3)解:如图,∠BMC+∠BNC=180°,
延长AB至F,过N,M分别作NG∥AB,MH∥AB,则有NG∥AB∥MH∥CD,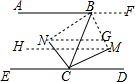
∴∠BNG=∠ABN,∠CNG=∠ECN,∠BMH=∠FBM,∠CMH=∠DCM,
∵BM⊥BN,CM⊥CN,
∴∠MBN=∠MCN=90°,
∵∠ABN+∠MBN+∠FBN=180°,∠ECN+∠MCN+∠DCM=180°,
∴∠ABN+∠FBM+∠ECN+∠DCM=180°,
∴∠BMC+∠BNC=∠BMH+∠CMH+∠BNG+∠CNG=∠ABN+∠FBM+∠ECN+∠DCM=180°,
∴∠BMC+∠BNC=180°不变.
点评 本题主要考查了角平分线的性质,作出恰当的辅助线是解答此题的关键.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
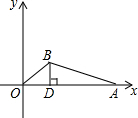 如图,在直角坐标系中,点A的坐标是(12,0),动直线OB与AB相交于点B,且BD⊥x轴于D,BD=3,则△OAB的周长的最小值是12+6$\sqrt{5}$.
如图,在直角坐标系中,点A的坐标是(12,0),动直线OB与AB相交于点B,且BD⊥x轴于D,BD=3,则△OAB的周长的最小值是12+6$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
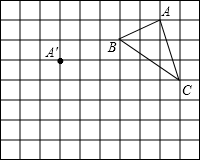 在正方形网格中,每个小正方形的边长均为1个单位长度,三角形ABC的三个顶点的位置如图所示,现将三角形ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.
在正方形网格中,每个小正方形的边长均为1个单位长度,三角形ABC的三个顶点的位置如图所示,现将三角形ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 观察下面一组数:-1,2,-3,4,-5,6,-7,….,将这组数排成如图的形式,按照如图规律排下去,则第11行中从左边数第10个数是( )
观察下面一组数:-1,2,-3,4,-5,6,-7,….,将这组数排成如图的形式,按照如图规律排下去,则第11行中从左边数第10个数是( )| A. | -110 | B. | 110 | C. | -111 | D. | 111 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
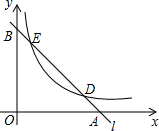 已知直线l分别与x轴、y轴交于A、B两点,与双曲线y=$\frac{m}{x}$(m≠0,x>0)分别交于D、E两点,若点D的坐标为(4,1),点E的坐标为(1,n)
已知直线l分别与x轴、y轴交于A、B两点,与双曲线y=$\frac{m}{x}$(m≠0,x>0)分别交于D、E两点,若点D的坐标为(4,1),点E的坐标为(1,n)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com