
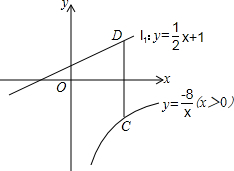 阅读理解:对于任意正实数a、b,∵${(\sqrt{a}-\sqrt{b})^2}$≥0,∴a-2$\sqrt{ab}$+b≥0,∴a+b≥2$\sqrt{ab}$,只有当a=b时,等号成立.
阅读理解:对于任意正实数a、b,∵${(\sqrt{a}-\sqrt{b})^2}$≥0,∴a-2$\sqrt{ab}$+b≥0,∴a+b≥2$\sqrt{ab}$,只有当a=b时,等号成立.分析 (1)由a+b≥2$\sqrt{p}$,只有当a=b时,a+b有最小值2$\sqrt{p}$,可求得当且仅当m=$\frac{1}{m}$时,m+$\frac{1}{m}$有最小值;
(2)由a+b≥2$\sqrt{p}$,只有当a=b时,a+b有最小值2$\sqrt{p}$,即可求得答案;
(3)首先设C$(n,\frac{-8}{n})$,则:D$(n,\frac{1}{2}n+1)$,即可表示出CD的长,再由若ab为定值p,则a+b≥2$\sqrt{p}$,只有当a=b时,a+b有最小值2$\sqrt{p}$,即可求得答案.
解答 解:(1)∵m>0,
∴m+$\frac{1}{m}$≥2$\sqrt{m•\frac{1}{m}}$=2,当且仅当m=$\frac{1}{m}$时,即m=1时,m+$\frac{1}{m}$有最小值,最小值为2;
故答案为:1,2;
(2)∵m>0,
∴2m+$\frac{8}{m}$≥2$\sqrt{2m•\frac{8}{m}}$=8,当且仅当2m=$\frac{8}{m}$时,即m=2时,2m+$\frac{8}{m}$有最小值,最小值为8;
故答案为:2,8
(3)设C$(n,\frac{-8}{n})$,则:D$(n,\frac{1}{2}n+1)$,
∴CD=$(\frac{1}{2}n+1)-\frac{-8}{n}=\frac{1}{2}n+\frac{8}{n}+1≥2\sqrt{\frac{1}{2}n•\frac{8}{n}}+1=5$,
∴CD最短为5,此时$\frac{1}{2}n=\frac{8}{n}$,n=4,
∴C(4,-2),D(4,3).
点评 此题属于反比例函数综合题.考查了几何不等式的应用以及一次函数与反比例函数上点的性质.注意理解几何不等式以及准确的应用是解此题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1<k<2 | B. | -1<k<1 | C. | 1<k<2 | D. | 1<k<3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
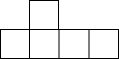 张明同学设计了某个产品的正方体包装盒如图所示,由于粗心少设计了其中一个顶盖,请你把它补上,使其成为一个两面均有盖的正方体盒子.
张明同学设计了某个产品的正方体包装盒如图所示,由于粗心少设计了其中一个顶盖,请你把它补上,使其成为一个两面均有盖的正方体盒子.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -8-(-3)=5 | B. | (-2.5)-(+7.2)=4.7 | C. | (-$\frac{2}{5}$)-(-$\frac{1}{4}$)=-$\frac{3}{20}$ | D. | 5-(-6)=-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com