
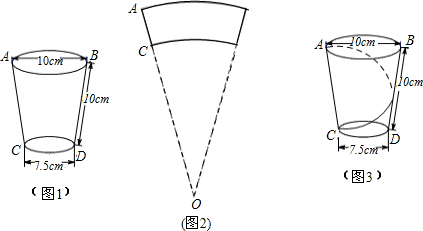
分析 (1)设∠O的度数是n,根据弧长公式得出10π=$\frac{nπ•OA}{180}$,7.5π=$\frac{nπ•(OA-10)}{180}$,求出OA和n即可;
(2)沿CA剪开,得出扇形AOA′,连接CA′,则CA′的长度是小虫爬行的最短路程,过C作CE⊥OA′于E,求出CE和OE,求出A′E,根据勾股定理求出CA′即可;
解答 解:(1)设∠O的度数是n,
则10π=$\frac{nπ•OA}{180}$,7.5π=$\frac{nπ•(OA-10)}{180}$,
解得:OA=40cm,n=45°;
(2)在图2中,沿CA剪开,得出扇形AOA′,连接CA′,则CA′的长度是小虫爬行的最短路程,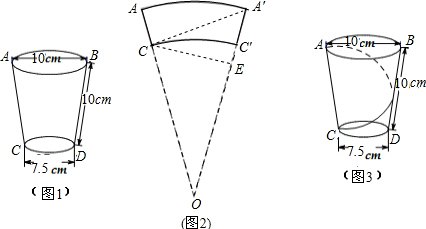
过C作CE⊥OA′于E,
在Rt△COE中,OC=30,∠O=45°,
∴CE=15$\sqrt{2}$,OE=15$\sqrt{2}$,
∴A′E=40-15$\sqrt{2}$,
在Rt△CEA′中,CA′=$\sqrt{{(40-15\sqrt{2})}^{2}{+(15\sqrt{2})}^{2}}$≈28cm.
故答案为:40,28.
点评 本题考查了平面展开-最短路线问题,矩形的性质,勾股定理,含45度角的直角三角形等知识点的综合运用,画出平面展开图是解答此题的关键.


科目:初中数学 来源: 题型:解答题
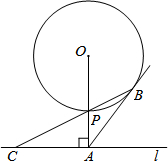 如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.
如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
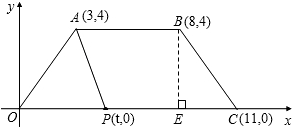 如图,在平面直角坐标系内,梯形OABC的顶点坐标分别是:A(3,4),B(8,4),C(11,0),点P(t,0)是线段OC上一点,设四边形ABCP的面积为S.
如图,在平面直角坐标系内,梯形OABC的顶点坐标分别是:A(3,4),B(8,4),C(11,0),点P(t,0)是线段OC上一点,设四边形ABCP的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50min才乘上缆车,缆车的平均速度为180m/min.设小亮出发x min后行走的路程为y m.图中的折线表示小亮在整个行走过程中y与x的函数关系.
小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50min才乘上缆车,缆车的平均速度为180m/min.设小亮出发x min后行走的路程为y m.图中的折线表示小亮在整个行走过程中y与x的函数关系.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com