
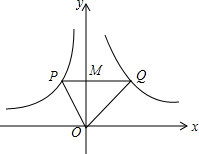
 如图,点P(-1,2)、Q(2,2)分别位于两个不同的双曲线上,则S△POQ=3.
如图,点P(-1,2)、Q(2,2)分别位于两个不同的双曲线上,则S△POQ=3. 分析 根据反比例函数比例系数k的几何意义得到S△OQM=2,S△OPM=1,然后利用S△POQ=S△OQM+S△OPM进行计算.
解答 解:设过点P(-1,2)的双曲线的解析式为:y=$\frac{m}{x}$,过点Q(2,2)双曲线的解析式为:y=$\frac{n}{x}$,
∴y=$\frac{-2}{x}$,y=$\frac{4}{x}$,
∵直线l∥x轴,
∴S△POQ=S△POM+S△QMO=$\frac{1}{2}×$2$+\frac{1}{2}×4$=3.
故答案为:3.
点评 本题考查了反比例函数比例系数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:解答题
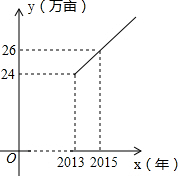 某市实施“农业立市,工业强市,旅游兴市”计划后,2013年全市荔枝种植面积为24万亩.调查分析结果显示:从2013年开始,该市荔枝种植面积y(万亩)随着时间x(年)逐年成直线上升,y与x之间的函数关系如图所示.
某市实施“农业立市,工业强市,旅游兴市”计划后,2013年全市荔枝种植面积为24万亩.调查分析结果显示:从2013年开始,该市荔枝种植面积y(万亩)随着时间x(年)逐年成直线上升,y与x之间的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
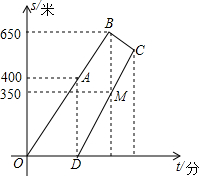 小明要在周日8点50分之前赶到距家1000米的书店去买书.早8点20分从家出发,8分钟后妈妈发现他忘了带钱包,于是立即出发按他走的路线去追.妈妈出发几分钟后,小明也发现了忘带钱包,于是按原路原速返回去取,几分钟后与妈妈相遇.假设在此过程中小明和妈妈的速度均保持不变,如图所示,给出两人离家距离s(米)和小明所走的时间t(分)之间的函数图象,结合图象回答下列问题:
小明要在周日8点50分之前赶到距家1000米的书店去买书.早8点20分从家出发,8分钟后妈妈发现他忘了带钱包,于是立即出发按他走的路线去追.妈妈出发几分钟后,小明也发现了忘带钱包,于是按原路原速返回去取,几分钟后与妈妈相遇.假设在此过程中小明和妈妈的速度均保持不变,如图所示,给出两人离家距离s(米)和小明所走的时间t(分)之间的函数图象,结合图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 胜一场 | 平一场 | 负一场 | |
| 积分 | 3 | 1 | 0 |
| 奖金(元/人) | 1300 | 500 | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com