
【题目】如图所示,边长为4的正方形ABCD绕点D逆时针旋转30°后能与四边形A′B′C′D′重合.
(1)旋转中心是哪一点?
(2)四边形A′B′C′D′,是怎样的图形?面积是多少?
(3)求∠C′DC和∠CDA′的度数;
(4)连接AA′,求∠DAA′的度数.

【答案】(1)点D(2)边长为4的正方形,16(3)30°,60°(4)75°
【解析】试题分析:(1)根据题意可得旋转中心是D点;
(2)因为四边形A′B′C′D′是由正方形ABCD旋转得到的,所以它是和四边形ABCD全等的正方形,边长还是4;
(3)根据旋转的宗旨即可得到;
(4)根据等腰三角形的性质即可求解.
试题解析:(1)旋转中心是点D.
(2)四边形A′B′C′D′是正方形,旋转不改变图形的大小,四边形A′B′C′D′是正方形ABCD旋转得来的,而正方形ABCD的面积为16,所以四边形A′B′C′D′的面积是16.
(3)因为C与C′是对应点,而对应点与旋转中心连线所成的角即是旋转角,由题意知图形绕点D旋转30°,所以∠C′DC=30°.又因为四边形A′B′C′D′是正方形,所以∠C′DA′=90°,而∠C′DC=30°,所以∠CDA′=60°.
(4)根据旋转的特征,对应点到旋转中心的距离相等,所以由点D,A,A′所确定的三角形是等腰三角形,AD=A′D,而∠ADA′=30°,所以∠DAA′=∠DA′A=(180°-30°)÷2=75°.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣ ![]() x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,比较适合用全面调查(普查)方式的是( ).
A.某灯具厂节能灯的使用寿命
B.全国居民年人均收入
C.某校今年初中生育体中考的成绩
D.全国快递包装产生的垃圾数量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中C点坐标为(1 ,2).
(1)写出点A、B的坐标:A( , )、B( , )
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A'B'C',则△A'B'C'的三个顶点坐标分别是A'( , )、B'( 、 )、 C'( 、 )

(3)计算△ABC的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形.
(1)如图(1)所示,点G是BC边上任意一点(不与B,C两点重合),连接AG,作BF⊥AG于点F,DE⊥AG于点E.求证△ABF≌△DAE;
(2)在(1)中,线段EF与AF,BF的等量关系是____;(不需证明,直接写出结论即可)
(3)如图(2)所示,若点G是CD边上任意一点(不与C,D两点重合),作BF⊥AG于点F,DE⊥AG于点E,那么图中的全等三角形是____,线段EF与AF,BF的等量关系是____.(不需证明,直接写出结论即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件:_____________,使△AEH≌△CEB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张长方形纸片分别沿着EP,FP对折,使B落在B′,C落在C′.
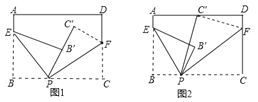
(1)若点P,B′,C′在同一直线上(图1),求两条折痕的夹角∠EPF的度数;
(2)若点P,B′,C′不在同一直线上(图2),且∠B′PC′=10°,求∠EPF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com