
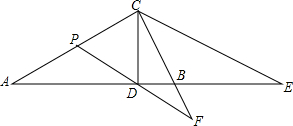
 如图,CD是△ABC的高,∠ACB=90°,∠DCB=∠ECB,P是AC的中点,PD的延长线交BC的延长线于点F,说明:AC•CE=2PF•CD.
如图,CD是△ABC的高,∠ACB=90°,∠DCB=∠ECB,P是AC的中点,PD的延长线交BC的延长线于点F,说明:AC•CE=2PF•CD. 分析 由CD是△ABC的高,得到∠CDE=∠ADC=90°,由于P是AC的中点,根据直角三角形的性质得到PD=AP=PC=$\frac{1}{2}$AC,根据外角的性质得到∠CPD=2∠A,根据已知条件得到∠DCE=2∠DCB=2∠A,推出△PCF∽△CDE,于是得到$\frac{CP}{CD}=\frac{PF}{CE}$,等量代换得到$\frac{1}{2}$AC•CE=PF•CD,于是得到结论.
解答 证明:∵CD是△ABC的高,
∴∠CDE=∠ADC=90°,
∵P是AC的中点,
∴PD=AP=PC=$\frac{1}{2}$AC,
∴∠A=∠PDA,
∠CPD=2∠A,
∵∠ACB=90°,
∴∠A=∠DCB,
∵∠DCB=∠ECB,
∴∠DCE=2∠DCB=2∠A,
∴∠CCPF=∠DCE,
∴△PCF∽△CDE,
∴$\frac{CP}{CD}=\frac{PF}{CE}$,
∴CP•CE=PF•CD,
∴$\frac{1}{2}$AC•CE=PF•CD,
∴AC•CE=2PF•CD.
点评 本题考查了相似三角形的判定和性质,直角三角形的性质,熟练掌握各定理是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
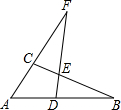 如图,△ABC中,D,E分别是AB和BC上的点,直线DE与AC的延长线交于点F,且AD•AB=AC•AF.求证:
如图,△ABC中,D,E分别是AB和BC上的点,直线DE与AC的延长线交于点F,且AD•AB=AC•AF.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
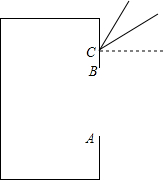 某地在一年中阳光与地面的最大角为60°,最小角为30°,当地的某一新建住宅区的住户准备统一在向阳的一边设计统一高度的窗,并在这些窗上方做一块“遮阳蓬”,如图所示.已知窗的统一高度AB为2米,试用你所学的知识,计算“遮阳蓬”CD应从窗的上方多高的点C伸出,伸出多长才能使房间内“冬暖夏凉”?
某地在一年中阳光与地面的最大角为60°,最小角为30°,当地的某一新建住宅区的住户准备统一在向阳的一边设计统一高度的窗,并在这些窗上方做一块“遮阳蓬”,如图所示.已知窗的统一高度AB为2米,试用你所学的知识,计算“遮阳蓬”CD应从窗的上方多高的点C伸出,伸出多长才能使房间内“冬暖夏凉”?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com