
【题目】某公司研发了一款成本为60元的保温饭盒,投放市场进行试销售,按物价部门规定,其销售单价不低于成本,但销售利润不高于65% .市场调研发现,保温饭盒每天的销售数量y(个)与销售单价x(元)满足一次函数关系;当销售单价为70元时,销售数量为160个;当销售单价为80元时,销售数量为140个(注:利润率=利润÷成本×100% ).
(1)求y与x之间的函数关系式;
(2)当销售单价定为多少元时,公司每天获得利润最大,最大利润为多少元?
【答案】(1)、y=-2x+300;(2)、销售单价定为99元时,公司每天获得利润最大,最大利润为3978元
【解析】
试题分析:(1)、首先设一次函数解析式为y=kx+b,根据题意利用待定系数法求出函数解析式;(2)、根据总利润=单件利润×数量得出函数解析式,然后将二次函数进行配方,然后根据函数的增减性得出最大值.
试题解析:(1)、设这个一次函数为y=kx+b(k≠0)
由题意知,![]() ,解得,
,解得,![]() . ∴
. ∴![]() 与
与![]() 的函数关系式是:y=﹣2x+300
的函数关系式是:y=﹣2x+300
(2)、当销售单价定为x元时,公司每天获得利润最大为W元,依题意得
W=(x﹣60)(﹣2x+300)=﹣2(x2﹣210x+9000)=﹣2(x﹣105)2+4050
因为按物价部门规定,其销售单价不低于成本,但销售利润不高于65%,因此销售单价最高只能定为99元
当x=99时,W有最大值3978元.
当销售单价定为99元时,公司每天获得利润最大,最大利润为3978元


科目:初中数学 来源: 题型:
【题目】设一个正方形的边长为acm,若边长增加3cm,则新正方形的面积增加了
A. 9cm2 B. 6acm2 C. (6a+9)cm2 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC是等腰直角三角形,∠BAC= 90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.
(1)当△ABC绕点A逆时针旋转![]() (0°<
(0°<![]() <90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长DB交CF于点H.
①求证: BD⊥CF. ② 当AB=2,AD=3,时,求线段BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BC相交于点P,BE与CD相交于点Q,连接PQ.
求证: (1)△ACD≌△BCE.
(2)△PCQ为等边三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一台自动测温记录仪记录的图象,它反映了我市春季气温T(℃)随时间t(时)变化而变化的关系,观察图象得到下列信息,其中错误的是( )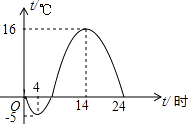
A.凌晨4时气温最低为﹣5℃
B.14时气温最高为16℃
C.从0时至14时,气温随时间推移而上升
D.从14时至24时,气温随时间推移而下降
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A. 若a=b,则a+c=b+c B. 若ac=bc,则a=b C. 若|a|=|b|,则a=b D. 若a2=b2,则a=b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个点在数轴上移动时,它所对应的数,也会有相应的变化.若点A先从原点开始,先向右移动1个单位长度,再向左移动3个单位长度,这时该点所对应的数是( )
A. 2 B. ﹣2 C. 8 D. ﹣8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com