
【题目】如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BC相交于点P,BE与CD相交于点Q,连接PQ.
求证: (1)△ACD≌△BCE.
(2)△PCQ为等边三角形.

科目:初中数学 来源: 题型:
【题目】某公司研发了一款成本为60元的保温饭盒,投放市场进行试销售,按物价部门规定,其销售单价不低于成本,但销售利润不高于65% .市场调研发现,保温饭盒每天的销售数量y(个)与销售单价x(元)满足一次函数关系;当销售单价为70元时,销售数量为160个;当销售单价为80元时,销售数量为140个(注:利润率=利润÷成本×100% ).
(1)求y与x之间的函数关系式;
(2)当销售单价定为多少元时,公司每天获得利润最大,最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周老师在一次“探究性学习”课中,设计了如下数表:
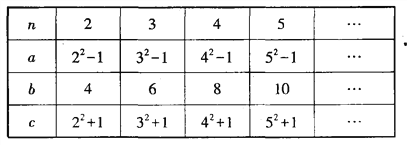
(1)请你分别观察a,b,c与n之间的关系,并用含自然数n(n>1)的代数式表示:
a=__ _____;b=___ ____;c=___ ____;
(2)猜想:以a,b,c为边长的三角形是否是直角三角形?证明你的猜想.
(3)、显然,满足这样关系的整数a、b、c我们把它叫做 数,请再写一组这样的数 (不同于表格中已出现的数组)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义符号min{a,b}的含义为:当a≥b时,min{a,b}=b;当a<b时,min{a,b}=a.如:min={1,﹣2}=﹣2,min{﹣1,2}=﹣1.则min{x2﹣1,﹣2}的值是( )
A.x2﹣1
B.2
C.﹣1
D.﹣2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com