
【题目】如图,已知点 ![]() 是线段
是线段 ![]() 上一点,
上一点,![]() ,
,![]() ,
,![]() .
.
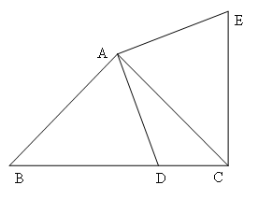
(1)线段 ![]() 绕点 逆时针旋转 °可与线段
绕点 逆时针旋转 °可与线段 ![]() 重合.
重合.
(2)若 ![]() ,则
,则 ![]() °.
°.
(3)若 ![]() ,
,![]() ,则
,则 ![]() .
.
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】如图,甲、乙为两座建筑物,它们之间的水平距离BC为30日,在A点测得D点的仰角∠EAD=45°,在B点测得D点的仰角为∠CBD=60°,测得甲、乙这两座建筑物的高度分别为( )米.

A. 10![]() ,30 B. 30,30
,30 B. 30,30![]() C. 30
C. 30![]() ﹣3,30 D. 30
﹣3,30 D. 30![]() ﹣30,30
﹣30,30![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
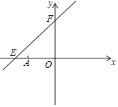
【题目】如图,直线y=kx+6与x轴、y轴分别相交于点E、F,点E的坐标为(-8,0),点A的坐标为(-6,0),点P是直线EF上的一个动点.
(1)求k的值;
(2)点P在第二象限内的直线EF上的运动过程中,写出△OPA的面积S与x的函整表达式,并写出自变量x的取值范围;
(3)探究,当点P在直线EF上运动到时,△OPA的面积可能是15吗,若能,请求出点P的坐标;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车的背面,有一种特殊形状的刮雨器,忽略刮雨器的宽度可抽象为一条折线![]() ,如图
,如图![]() 所示,量得连杆
所示,量得连杆![]() 长为
长为![]() ,雨刮杆
,雨刮杆![]() 长为
长为![]() ,
,![]() .若启动一次刮雨器,雨刮杆
.若启动一次刮雨器,雨刮杆![]() 正好扫到水平线
正好扫到水平线![]() 的位置,如图
的位置,如图![]() 所示.
所示.

![]() 求雨刮杆
求雨刮杆![]() 旋转的最大角度及
旋转的最大角度及![]() 、
、![]() 两点之间的距离;
两点之间的距离;
![]() 求雨刮杆
求雨刮杆![]() 扫过的最大面积.
扫过的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一组数9,17,25,33,…,(8n+1)(从左往右数,第1个数是9,第2个数是17,第3个数是25,第4个数是33,依此类推,第n个数是8n+1).设这组数的前n个数的和是sn.
(1)第5个数是多少?并求1892—s5的值;
(2)若n满足方程![]() =
=![]() ,则
,则![]() 的值是整数吗?请说明理由.
的值是整数吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
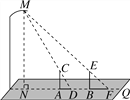
【题目】晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞.小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ移动,如图,当小聪正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小军正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小军身高BE的长(结果精确到0.01米).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y1=![]() 的图象与一次函数y2=
的图象与一次函数y2=![]() 的图象交于点A,B,点B的横坐标实数4,点P(1,m)在反比例函数y1=
的图象交于点A,B,点B的横坐标实数4,点P(1,m)在反比例函数y1=![]() 的图象上.
的图象上.
(1)求反比例函数的表达式;
(2)观察图象回答:当x为何范围时,y1>y2;
(3)求△PAB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象经过点(2,3),顶点坐标(1,4)
(1)求该二次函数的解析式;
(2)图象与x轴的交点为A、B,与y轴的交点为C,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com