【题目】梦洁和嘉丽是邻居，星期天他们两家人准备去郊外的农家乐游玩，早上两家人同时乘坐了两辆不同价格的出租车，梦洁家乘坐的是起步4公里8元，以后每公里收1.2元，嘉丽家乘坐的是起步3公里6元，以后每公里收1.3元，两家人几乎同时到达农家乐，付款后梦洁发现两家人的车费仅差1.5元，则两家住地离公园的路程是( )
A.
公里B.
公里C.
公里D.
公里
科目：初中数学 来源： 题型：
【题目】如图，已知A，B两点在数轴上，点A表示的数为-10，OB=3OA，点M以每秒3个单位长度的速度从点A向右运动．点N以每秒2个单位长度的速度从点O向右运动（点M、点N同时出发）
（1）数轴上点B对应的数是______．
（2）经过几秒，点M、点N分别到原点O的距离相等？
（3）当点M运动到什么位置时，恰好使AM=2BN？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，二次函数
的图象经过A(2，0)，B(0，－6)两点．
（1）求这个二次函数的解析式；
（2）设该二次函数的对称轴与x轴交于点C，连接BA，BC，求△ABC的面积．
（3）在x轴上是否存在一点P，使△ABP为等腰三角形，若存在，求出P的坐标，若不存在，说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=﹣1，且抛物线经过A（1，0），C（0，3）两点，与x轴交于点B．
（1）若直线y=mx+n经过B、C两点，求直线BC和抛物线的解析式；
（2）在抛物线的对称轴x=﹣1上找一点M，使点M到点A的距离与到点C的距离之和最小，求出点M的坐标；
（3）设点P为抛物线的对称轴x=﹣1上的一个动点，求使△BPC为直角三角形的点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，⊿ABC中，∠A=40°，∠ACB=104°，BD为AC边上的高，BE是⊿ABC的角平分线，求∠EBD的度数．
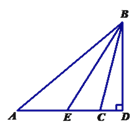
【答案】32°
【解析】试题分析：根据三角形的内角和定理求出∠ABC，再根据角平分线的定义求出∠ABE，然后利用三角形的一个外角等于与它不相邻的两个内角的和列式求出∠BED，再根据直角三角形两锐角互余列式进行计算即可得解．
试题解析：由三角形内角和定理，得∠B+∠ACB+∠BAC=180°，
又∠A=40°，∠ACB=104°，
∴∠ABC=180°-40°-104°=36°，
又∵BE平分∠ABC，
∴∠ABE=
∠ABC=18°
∴∠BED=∠A+∠ABE=40°+18°=58°，
又∵∠BED+∠DBE=90°，
∴∠DBE=90°-∠BED=90°-58°=32°．
【题型】解答题
【结束】
25
【题目】已知,如图, AB∥CD，∠1=∠2，那么∠E和∠F相等吗? 为什么?
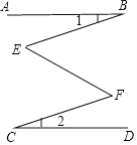
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线SN与直线WE相交于点O，射线ON表示正北方向，射线OE表示正东方向.已知射线OB的方向是南偏东56°，射线 OC在∠NOE内，且∠NOC与∠BOS互余，射线OA平分∠BON，图中与∠COA互余的角是________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，直线l1：
分别与x轴、y轴交于点B、C，且与直线l2：
交于点A．
（1）求出点A的坐标
（2）若D是线段OA上的点，且△COD的面积为12，求直线CD的解析式
（3）在（2）的条件下，设P是射线CD上的点，在平面内是否存在点Q，使以O、C、P、Q为顶点的四边形是菱形？若存在，直接写出点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若数a使关于x的分式方程
的解为正数，且使关于y的不等式组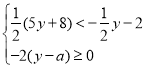
的解集为y＜﹣2，则符合条件的所有整数a的和为（ ）
A. 10B. 12C. 14D. 16
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：在平面直角坐标系中，过一点分别作坐标轴的垂线，若与坐标轴围成矩形的周长与面积在数量上相等，则这个点叫做和谐点．
（1）判断点M（﹣1，2），N（﹣4，﹣4）是否为和谐点，并说明理由；
（2）若和谐点P（a，3）在直线y=﹣x+b（b为常数）上，试求a，b的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
