
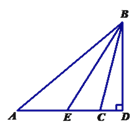
【题目】如图,⊿ABC中,∠A=40°,∠ACB=104°,BD为AC边上的高,BE是⊿ABC的角平分线,求∠EBD的度数.
【答案】32°
【解析】试题分析:根据三角形的内角和定理求出∠ABC,再根据角平分线的定义求出∠ABE,然后利用三角形的一个外角等于与它不相邻的两个内角的和列式求出∠BED,再根据直角三角形两锐角互余列式进行计算即可得解.
试题解析:由三角形内角和定理,得∠B+∠ACB+∠BAC=180°,
又∠A=40°,∠ACB=104°,
∴∠ABC=180°-40°-104°=36°,
又∵BE平分∠ABC,
∴∠ABE=![]() ∠ABC=18°
∠ABC=18°
∴∠BED=∠A+∠ABE=40°+18°=58°,
又∵∠BED+∠DBE=90°,
∴∠DBE=90°-∠BED=90°-58°=32°.
【题型】解答题
【结束】
25
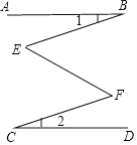
【题目】已知,如图, AB∥CD,∠1=∠2,那么∠E和∠F相等吗? 为什么?
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
某中学为迎接校运会,筹集7000元购买了甲、乙两种品牌的篮球共30个,其中购买甲品牌篮球花费3000元,已知甲品牌篮球比乙品牌篮球的单价高50%,求乙品牌篮球的单价及个数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标平面内,已点A(3,0)、B(-5,3),将点A向左平移6个单位到达C点,将点B向下平移6个单位到达D点.
(1)写出C点、D点的坐标:C __________,D ____________ ;
(2)把这些点按A-B-C-D-A顺次连接起来,这个图形的面积是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.
(1)求证:BE=CE;
(2)试判断四边形BFCD的形状,并说明理由;
(3)若BC=8,AD=10,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求符合下列条件的抛物线的解析式:
(1)将抛物线y=-x2先向上平移1个单位长度,再绕其顶点旋转180°;
(2)抛物线y=ax2+1经过点(1,0);
(3)抛物线y=ax2-1与直线y=![]() x+3的一个交点是(2,m).
x+3的一个交点是(2,m).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,以BC为直径的⊙O交AB于点D,AE平分∠BAC交BC于点E,交CD于点F.且CE=CF.
(1)求证:直线CA是⊙O的切线;
(2)若BD=![]() DC,求
DC,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根,
(1)试推导x1+x2=-![]() ,x1·x2=
,x1·x2=![]() ;
;
(2)求代数式a(x13+x23)+b(x12+x22)+c(x1+x2)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com