
【题目】设x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根,
(1)试推导x1+x2=-![]() ,x1·x2=
,x1·x2=![]() ;
;
(2)求代数式a(x13+x23)+b(x12+x22)+c(x1+x2)的值.
科目:初中数学 来源: 题型:
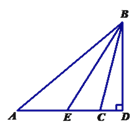
【题目】如图,⊿ABC中,∠A=40°,∠ACB=104°,BD为AC边上的高,BE是⊿ABC的角平分线,求∠EBD的度数.
【答案】32°
【解析】试题分析:根据三角形的内角和定理求出∠ABC,再根据角平分线的定义求出∠ABE,然后利用三角形的一个外角等于与它不相邻的两个内角的和列式求出∠BED,再根据直角三角形两锐角互余列式进行计算即可得解.
试题解析:由三角形内角和定理,得∠B+∠ACB+∠BAC=180°,
又∠A=40°,∠ACB=104°,
∴∠ABC=180°-40°-104°=36°,
又∵BE平分∠ABC,
∴∠ABE=![]() ∠ABC=18°
∠ABC=18°
∴∠BED=∠A+∠ABE=40°+18°=58°,
又∵∠BED+∠DBE=90°,
∴∠DBE=90°-∠BED=90°-58°=32°.
【题型】解答题
【结束】
25
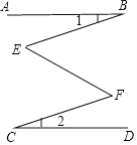
【题目】已知,如图, AB∥CD,∠1=∠2,那么∠E和∠F相等吗? 为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,,直线MN分别与x轴、y轴交于点M(6,0),N(0, ![]() ),等边△ABC的顶点B与原点O重合,BC边落在x轴正半轴上,点A恰好落在线段MN上,将等边△ABC从图l的位置沿x轴正方向以每秒l个单位长度的速度平移,边AB,AC分别与线段MN交于点E,F(如图2所示),设△ABC平移的时间为t(s).
),等边△ABC的顶点B与原点O重合,BC边落在x轴正半轴上,点A恰好落在线段MN上,将等边△ABC从图l的位置沿x轴正方向以每秒l个单位长度的速度平移,边AB,AC分别与线段MN交于点E,F(如图2所示),设△ABC平移的时间为t(s).
(1)等边△ABC的边长为_______;
(2)在运动过程中,当t=_______时,MN垂直平分AB;
(3)若在△ABC开始平移的同时.点P从△ABC的顶点B出发.以每秒2个单位长度的速度沿折线BA—AC运动.当点P运动到C时即停止运动.△ABC也随之停止平移.
①当点P在线段BA上运动时,若△PEF与△MNO相似.求t的值;
②当点P在线段AC上运动时,设![]() ,求S与t的函数关系式,并求出S的最大值及此时点P的坐标.
,求S与t的函数关系式,并求出S的最大值及此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AGF=∠ABC,∠1+∠2=180°.
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A. 周长相等的锐角三角形都全等 B. 周长相等的直角三角形都全等
C. 周长相等的钝角三角形都全等 D. 周长相等的等腰直角三角形都全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将三角形各顶点的纵坐标都减去1,横坐标保持不变,所得图形与原图形相比是( )
A.向下平移了1个单位B.向上平移了1个单位
C.向左平移了1个单位D.向右平移了1个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程![]() mx-3x+m-4=0(m为常数).
mx-3x+m-4=0(m为常数).
(1)求证:方程有两个不相等的实数根;
(2)设![]() ,
,![]() 是方程的两个实数根,且
是方程的两个实数根,且![]() +
+![]() =6.请求出方程的这两个实数根.
=6.请求出方程的这两个实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB 是⊙O 的直径,点C 是⊙O 上一点,AD 与过点C的切线垂直,垂足为 D,直线 DC 与AB 的延长线相交于点P,弦CE 平分∠ACB,交AB 于点F,连接BE.

求证:(1)AC 平分∠DAB;
(2)△PCF 是等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com