
【题目】已知关于x的方程![]() mx-3x+m-4=0(m为常数).
mx-3x+m-4=0(m为常数).
(1)求证:方程有两个不相等的实数根;
(2)设![]() ,
,![]() 是方程的两个实数根,且
是方程的两个实数根,且![]() +
+![]() =6.请求出方程的这两个实数根.
=6.请求出方程的这两个实数根.
【答案】(1)证明见解析(2)x1=3+![]() , x2=3-
, x2=3-![]()
【解析】试题分析:(1)根据根的判别式△=(-m-3)2-4(m-4)=m2+2m+25=(m+1)2+24,证明△>0,即方程有两个不相等的实数根;
(2)首先根据x1+x2=6求出m的值,然后根据公式法求出方程的两个根.
试题解析:(1)证明:∵关于x的方程x2-mx-3x+m-4=0(m为常数),
∴此方程为x2-(m+3)x+m-4=0,
∴△=(-m-3)2-4(m-4)=m2+2m+25=(m+1)2+24,
∴△>0,
∴关于x的方程x2-mx-3x+m-4=0有两个不相等的实数根;
(2)解:∵x1,x2是方程的两个实数根,
∴x1+x2=m+3,x1x2=m-4,
∵x1+x2=6,
∴m+3=6,
∴m=3,
∴原一元二次方程为:x2-6x-1=0,
解得x1=![]() ,x2=
,x2=![]() ,
,
∴此方程两根分别为:x1=![]() ,x2=
,x2=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,以BC为直径的⊙O交AB于点D,AE平分∠BAC交BC于点E,交CD于点F.且CE=CF.
(1)求证:直线CA是⊙O的切线;
(2)若BD=![]() DC,求
DC,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根,
(1)试推导x1+x2=-![]() ,x1·x2=
,x1·x2=![]() ;
;
(2)求代数式a(x13+x23)+b(x12+x22)+c(x1+x2)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣2(k﹣1)x+k2=0有两个实数根x1,x2.
(1)求k的取值范围;
(2)若|x1+x2|=x1x2﹣1,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:对于平面图形A,如果存在一个圆,使图形A上的任意一点到圆心的距离都不大于这个圆的半径,则称图形A被这个圆所覆盖.回答下列问题:
(1)边长为1cm的正方形被一个半径为r的圆所覆盖,r的最小值是______ cm;
(2)边长为1cm的等边三角形被一个半径为r的圆所覆盖,r的最小值是______ cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
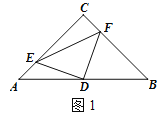
【题目】如图,△ABC中,AC=BC,∠C=90°,点D是AB的中点.
(1)如图1,若点E、F分别是AC、BC上的点,且AE=CF,请判别△DEF的形状,并说明理由;
(2)若点E、F分别是CA、BC延长线上的点,且AE=CF,则(1)中的结论是否仍然成立?请
说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中不正确的是( )
A. 抛掷一枚硬币,硬币落地时正面朝上是随机事件
B. 把4个球放入三个抽屉中,其中一个抽屉中至少有2个球是必然事件
C. 任意打开七年级下册数学教科书,正好是97页是确定事件
D. 一个盒子中有白球m个,红球6个,黑球n个(每个除了颜色外都相同).如果从中任取一个球,取得的是红球的概率与不是红球的概率相同,那么m与n的和是6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com