
【题目】如图,△ABC中,AC=BC,∠C=90°,点D是AB的中点.
(1)如图1,若点E、F分别是AC、BC上的点,且AE=CF,请判别△DEF的形状,并说明理由;
(2)若点E、F分别是CA、BC延长线上的点,且AE=CF,则(1)中的结论是否仍然成立?请
说明理由.
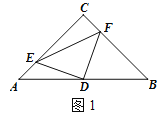
【答案】(1)△DEF是等腰直角三角形. (2)仍然成立.
【解析】试题分析:
(1)连接CD,如图1,结合已知条件易证△AED≌△CFD,由此即可证得DE=DF,∠EDF=90°,从而可得△DEF是等腰直角三角形;
(2)先根据题意画出符合要求的图形,如图2,连接CD,结合已知条件易证△AED≌△CFD,由此即可证得;DE=DF,∠EDF=90°,从而可得此时△DEF仍然是等腰直角三角形.
试题解析:
(1)△DEF是等腰直角三角形,理由如下:
如图1,连接CD,
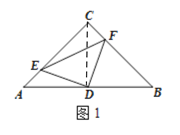
∵AC=BC,∠ACB=90°,点D是BC边的中点,
∴CD⊥BC,∠A=∠DCF=45°,CD=![]() BC=AD,
BC=AD,
又∵AE=CF,
∴△AED≌△CFD,
∴DE=DF,∠ADE=∠CDF,
又∵CD⊥BC,
∴∠CFD+∠CDE=∠ADE+∠CDE=∠CDA=90°,即∠EDF=90°,
∴△DEF是等腰直角三角形;
(2)如图2,(1)中结论仍然成立,理由如下:
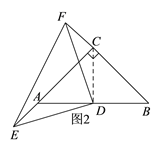
连接CD,∵AC=BC,∠ACB=90°,点D是BC边的中点,
∴CD⊥BC,∠A=∠DCB=45°,CD=![]() BC=AD,
BC=AD,
∴∠EAD=180°+45°=135°,∠ACD=180°-45°=135°,
又∵AE=CF,
∴△AED≌△CFD,
∴DE=DF,∠ADE=∠CDF,
又∵CD⊥BC,
∴∠ADE+∠ADF=∠CDF+∠ADF=∠CDA=90°,即∠EDF=90°,
∴△DEF是等腰直角三角形;


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,,直线MN分别与x轴、y轴交于点M(6,0),N(0, ![]() ),等边△ABC的顶点B与原点O重合,BC边落在x轴正半轴上,点A恰好落在线段MN上,将等边△ABC从图l的位置沿x轴正方向以每秒l个单位长度的速度平移,边AB,AC分别与线段MN交于点E,F(如图2所示),设△ABC平移的时间为t(s).
),等边△ABC的顶点B与原点O重合,BC边落在x轴正半轴上,点A恰好落在线段MN上,将等边△ABC从图l的位置沿x轴正方向以每秒l个单位长度的速度平移,边AB,AC分别与线段MN交于点E,F(如图2所示),设△ABC平移的时间为t(s).
(1)等边△ABC的边长为_______;
(2)在运动过程中,当t=_______时,MN垂直平分AB;
(3)若在△ABC开始平移的同时.点P从△ABC的顶点B出发.以每秒2个单位长度的速度沿折线BA—AC运动.当点P运动到C时即停止运动.△ABC也随之停止平移.
①当点P在线段BA上运动时,若△PEF与△MNO相似.求t的值;
②当点P在线段AC上运动时,设![]() ,求S与t的函数关系式,并求出S的最大值及此时点P的坐标.
,求S与t的函数关系式,并求出S的最大值及此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将三角形各顶点的纵坐标都减去1,横坐标保持不变,所得图形与原图形相比是( )
A.向下平移了1个单位B.向上平移了1个单位
C.向左平移了1个单位D.向右平移了1个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程![]() mx-3x+m-4=0(m为常数).
mx-3x+m-4=0(m为常数).
(1)求证:方程有两个不相等的实数根;
(2)设![]() ,
,![]() 是方程的两个实数根,且
是方程的两个实数根,且![]() +
+![]() =6.请求出方程的这两个实数根.
=6.请求出方程的这两个实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ⊙O 的半径是2,直线l与⊙O 相交于A、B 两点,M、N 是⊙O 上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB 面积的最大值是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB 是⊙O 的直径,点C 是⊙O 上一点,AD 与过点C的切线垂直,垂足为 D,直线 DC 与AB 的延长线相交于点P,弦CE 平分∠ACB,交AB 于点F,连接BE.

求证:(1)AC 平分∠DAB;
(2)△PCF 是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题为假命题的是( )
A.垂线段最短
B.两条直线相交,若邻补角相等,则这两条直线互相垂直
C.相等的角是对顶角
D.经过直线外一点,有且只有一条直线与这条直线平行
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com