
ЎҫМвДҝЎҝИзНј1Ј¬ФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬Ј¬ЦұПЯMN·ЦұрУлxЦбЎўyЦбҪ»УЪөгMЈЁ6Ј¬0Ј©Ј¬NЈЁ0Ј¬ ![]() Ј©Ј¬өИұЯЎчABCөД¶ҘөгBУлФӯөгOЦШәПЈ¬BCұЯВдФЪxЦбХэ°лЦбЙПЈ¬өгAЗЎәГВдФЪПЯ¶ОMNЙПЈ¬Ҫ«өИұЯЎчABCҙУНјlөДО»ЦГСШxЦбХэ·ҪПтТФГҝГлlёцөҘО»іӨ¶ИөДЛЩ¶ИЖҪТЖЈ¬ұЯABЈ¬AC·ЦұрУлПЯ¶ОMNҪ»УЪөгEЈ¬FЈЁИзНј2ЛщКҫЈ©Ј¬ЙиЎчABCЖҪТЖөДКұјдОӘtЈЁsЈ©Ј®
Ј©Ј¬өИұЯЎчABCөД¶ҘөгBУлФӯөгOЦШәПЈ¬BCұЯВдФЪxЦбХэ°лЦбЙПЈ¬өгAЗЎәГВдФЪПЯ¶ОMNЙПЈ¬Ҫ«өИұЯЎчABCҙУНјlөДО»ЦГСШxЦбХэ·ҪПтТФГҝГлlёцөҘО»іӨ¶ИөДЛЩ¶ИЖҪТЖЈ¬ұЯABЈ¬AC·ЦұрУлПЯ¶ОMNҪ»УЪөгEЈ¬FЈЁИзНј2ЛщКҫЈ©Ј¬ЙиЎчABCЖҪТЖөДКұјдОӘtЈЁsЈ©Ј®
ЈЁ1Ј©өИұЯЎчABCөДұЯіӨОӘ_______Ј»
ЈЁ2Ј©ФЪФЛ¶Ҝ№эіМЦРЈ¬өұt=_______КұЈ¬MNҙ№ЦұЖҪ·ЦABЈ»
ЈЁ3Ј©ИфФЪЎчABCҝӘКјЖҪТЖөДН¬КұЈ®өгPҙУЎчABCөД¶ҘөгBіц·ўЈ®ТФГҝГл2ёцөҘО»іӨ¶ИөДЛЩ¶ИСШХЫПЯBAЎӘACФЛ¶ҜЈ®өұөгPФЛ¶ҜөҪCКұјҙНЈЦ№ФЛ¶ҜЈ®ЎчABCТІЛжЦ®НЈЦ№ЖҪТЖЈ®
ўЩөұөгPФЪПЯ¶ОBAЙПФЛ¶ҜКұЈ¬ИфЎчPEFУлЎчMNOПаЛЖЈ®ЗуtөДЦөЈ»
ўЪөұөгPФЪПЯ¶ОACЙПФЛ¶ҜКұЈ¬Йи![]() Ј¬ЗуSУлtөДәҜКэ№ШПөКҪЈ¬ІўЗуіцSөДЧоҙуЦөј°ҙЛКұөгPөДЧшұкЈ®
Ј¬ЗуSУлtөДәҜКэ№ШПөКҪЈ¬ІўЗуіцSөДЧоҙуЦөј°ҙЛКұөгPөДЧшұкЈ®

Ўҫҙр°ёЎҝЈЁ1Ј©3Ј»ЈЁ2Ј©3Ј»ЈЁ3Ј©ўЩt=1»т![]() »т
»т![]() Ј»ўЪS=
Ј»ўЪS= ![]() Ј¬өұt=
Ј¬өұt=![]() КұЈ¬ЎчPEFөДГж»эЧоҙуЈ¬ЧоҙуЦөОӘ
КұЈ¬ЎчPEFөДГж»эЧоҙуЈ¬ЧоҙуЦөОӘ![]() Ј¬ҙЛКұPЈЁ3Ј¬
Ј¬ҙЛКұPЈЁ3Ј¬ ![]() Ј©Ј®
Ј©Ј®
ЎҫҪвОцЎҝКФМв·ЦОцЈәЈЁ1Ј©ёщҫЭЈ¬ЎПOMN=30ЎгәНЎчABCОӘөИұЯИэҪЗРОЈ¬ЗуЦӨЎчOAMОӘЦұҪЗИэҪЗРОЈ¬И»әујҙҝЙөГіцҙр°ёЈ®
ЈЁ2Ј©ТЧЦӘөұөгCУлMЦШәПКұЦұПЯMNЖҪ·ЦПЯ¶ОABЈ¬ҙЛКұOB=3Ј¬УЙҙЛјҙҝЙҪвҫцОКМвЈ»
ЈЁ3Ј©ўЩИзНј1ЦРЈ¬УЙМвТвBP=2tЈ¬BM=6©ҒtЈ¬УЙЎчPEFУлЎчMNOПаЛЖЈ¬ҝЙөГ![]() =
=![]() »т
»т![]() =
=![]() Ј¬јҙ
Ј¬јҙ![]() =
=![]() »т
»т![]() =
=![]() Ј¬Ҫв·ҪіМјҙҝЙҪвҫцОКМвЈ»
Ј¬Ҫв·ҪіМјҙҝЙҪвҫцОКМвЈ»
ўЪөұPөгФЪEFЙП·ҪКұЈ¬№эPЧчPHЎНMNУЪHЈ¬ИзНј2ЦРЈ¬№№ҪЁ¶юҙОәҜКэАыУГ¶юҙОәҜКэөДРФЦКјҙҝЙҪвҫцОКМвЈ»
КФМвҪвОцЈәҪвЈәЈЁ1Ј©ЎЯЦұПЯMN·ЦұрУлxЦбХэ°лЦбЎўyЦбХэ°лЦбҪ»УЪөгMЎўNЈ¬OM=6cmЈ¬ON=![]() Ј¬ЎаtanЎПOMN=
Ј¬ЎаtanЎПOMN=![]() =
=![]() Ј¬ЎаЎПOMN=30ЎгЈ¬ЎаЎПONM=60ЎгЈ¬ЎЯЎчABCОӘөИұЯИэҪЗРОЈ¬ЎаЎПAOC=60ЎгЈ¬ЎПNOA=30ЎгЈ¬ЎаOAЎНMNЈ¬јҙЎчOAMОӘЦұҪЗИэҪЗРОЈ¬ЎаOA=
Ј¬ЎаЎПOMN=30ЎгЈ¬ЎаЎПONM=60ЎгЈ¬ЎЯЎчABCОӘөИұЯИэҪЗРОЈ¬ЎаЎПAOC=60ЎгЈ¬ЎПNOA=30ЎгЈ¬ЎаOAЎНMNЈ¬јҙЎчOAMОӘЦұҪЗИэҪЗРОЈ¬ЎаOA=![]() OM=
OM=![]() ЎБ6=3Ј®№Кҙр°ёОӘЈә3Ј®
ЎБ6=3Ј®№Кҙр°ёОӘЈә3Ј®
ЈЁ2Ј©ТЧЦӘөұөгCУлMЦШәПКұЦұПЯMNЖҪ·ЦПЯ¶ОABЈ¬ҙЛКұOB=3Ј¬ЛщТФt=3Ј®№Кҙр°ёОӘЈә3Ј®
ЈЁ3Ј©ўЩИзНј1ЦРЈ¬УЙМвТвBP=2tЈ¬BM=6©ҒtЈ¬ЎЯЎПBEM=90ЎгЈ¬ЎПBME=30ЎгЈ¬ЎаBE=3©Ғ![]() Ј¬AE=AB©ҒBE=
Ј¬AE=AB©ҒBE=![]() Ј¬ЎЯЎПBAC=60ЎгЈ¬ЎаEF=
Ј¬ЎЯЎПBAC=60ЎгЈ¬ЎаEF=![]() AE=
AE=![]() tЈ¬өұөгPФЪEFПВ·ҪКұЈ¬PE=BE©ҒBP=3©Ғ
tЈ¬өұөгPФЪEFПВ·ҪКұЈ¬PE=BE©ҒBP=3©Ғ![]() tЈ¬УЙ
tЈ¬УЙ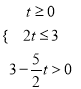 Ј¬ҪвөГ0ЎЬtЈј
Ј¬ҪвөГ0ЎЬtЈј![]() Ј¬ЎЯЎчPEFУлЎчMNOПаЛЖЈ¬Ўа
Ј¬ЎЯЎчPEFУлЎчMNOПаЛЖЈ¬Ўа![]() =
=![]() »т
»т![]() =
=![]() Ј¬Ўа
Ј¬Ўа![]() =
=![]() »т
»т![]() =
=![]() Ј¬ҪвөГt=1»тt=
Ј¬ҪвөГt=1»тt=![]() Ј®
Ј®
өұөгPФЪEFЙП·ҪКұЈ¬PE=BE©ҒBP=![]() t-3Ј¬ЎЯЎчPEFУлЎчMNOПаЛЖЈ¬Ўа
t-3Ј¬ЎЯЎчPEFУлЎчMNOПаЛЖЈ¬Ўа![]() =
=![]() »т
»т![]() =
=![]() Ј¬Ўа
Ј¬Ўа![]() =
=![]() »т
»т![]() =
=![]() Ј¬ҪвөГt=
Ј¬ҪвөГt=![]() »т3Ј®ЎЯ0ЎЬtЎЬ
»т3Ј®ЎЯ0ЎЬtЎЬ![]() Ј¬ЗТ
Ј¬ЗТ![]() t-3Јҫ0Ј¬јҙ
t-3Јҫ0Ј¬јҙ![]() ЈјtЎЬ
ЈјtЎЬ![]() Ј¬Ўаt=
Ј¬Ўаt=![]() .
.
ЧЫЙПЛщКцЈ¬t=1»т![]() »т
»т![]() Ј®
Ј®

ўЪөұPөгФЪEFЙП·ҪКұЈ¬№эPЧчPHЎНMNУЪHЈ¬ИзНј2ЦРЈ¬УЙМвТвЈ¬EF=![]() tЈ¬FC=MC=3©ҒtЈ¬ЎПPFH=30ЎгЈ¬ЎаPF=PC©ҒCF=ЈЁ6©Ғ2tЈ©©ҒЈЁ3©ҒtЈ©=3©ҒtЈ¬ЎаPH=
tЈ¬FC=MC=3©ҒtЈ¬ЎПPFH=30ЎгЈ¬ЎаPF=PC©ҒCF=ЈЁ6©Ғ2tЈ©©ҒЈЁ3©ҒtЈ©=3©ҒtЈ¬ЎаPH=![]() PF=
PF=![]() Ј¬ЎаS=
Ј¬ЎаS=![]() EFPH=
EFPH=![]() ЎБ
ЎБ![]() tЎБ
tЎБ![]() =
= ![]() =
=![]() Ј¬ЎЯ
Ј¬ЎЯ![]() ЎЬtЎЬ3Ј¬Ўаөұt=
ЎЬtЎЬ3Ј¬Ўаөұt=![]() КұЈ¬ЎчPEFөДГж»эЧоҙуЈ¬ЧоҙуЦөОӘ
КұЈ¬ЎчPEFөДГж»эЧоҙуЈ¬ЧоҙуЦөОӘ![]() Ј¬ҙЛКұPЈЁ3Ј¬
Ј¬ҙЛКұPЈЁ3Ј¬ ![]() Ј©Ј¬өұt=3КұЈ¬өгPУлFЦШәПЈ¬№КPөгФЪEFПВ·ҪІ»іЙБўЈ®
Ј©Ј¬өұt=3КұЈ¬өгPУлFЦШәПЈ¬№КPөгФЪEFПВ·ҪІ»іЙБўЈ®
№КS= ![]() Ј¬өұt=
Ј¬өұt=![]() КұЈ¬ЎчPEFөДГж»эЧоҙуЈ¬ЧоҙуЦөОӘ
КұЈ¬ЎчPEFөДГж»эЧоҙуЈ¬ЧоҙуЦөОӘ![]() Ј¬ҙЛКұPЈЁ3Ј¬
Ј¬ҙЛКұPЈЁ3Ј¬ ![]() Ј©Ј®
Ј©Ј®


 ГыКҰЦёөјТ»ҫнНЁПөБРҙр°ё
ГыКҰЦёөјТ»ҫнНЁПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФІOөДЦұҫ¶ABОӘ13cmЈ¬ПТACОӘ5cmЈ¬ЎПACBөДЖҪ·ЦПЯФІOУЪDЈ¬ФтCDіӨКЗ_______cm

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЗу·ыәППВБРМхјюөДЕЧОпПЯөДҪвОцКҪЈә
(1)Ҫ«ЕЧОпПЯyЈҪЈӯx2ПИПтЙПЖҪТЖ1ёцөҘО»іӨ¶ИЈ¬ФЩИЖЖд¶ҘөгРэЧӘ180ЎгЈ»
(2)ЕЧОпПЯyЈҪax2Ј«1ҫӯ№эөг(1Ј¬0)Ј»
(3)ЕЧОпПЯyЈҪax2Јӯ1УлЦұПЯyЈҪ![]() xЈ«3өДТ»ёцҪ»өгКЗ(2Ј¬m)Ј®
xЈ«3өДТ»ёцҪ»өгКЗ(2Ј¬m)Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ЎчABCЦРЈ¬ТФBCОӘЦұҫ¶өДЎСOҪ»ABУЪөгDЈ¬AEЖҪ·ЦЎПBACҪ»BCУЪөгEЈ¬Ҫ»CDУЪөгFЈ®ЗТCE=CFЈ®
ЈЁ1Ј©ЗуЦӨЈәЦұПЯCAКЗЎСOөДЗРПЯЈ»
ЈЁ2Ј©ИфBD=![]() DCЈ¬Зу
DCЈ¬Зу![]() өДЦөЈ®
өДЦөЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘЎП1ЈҪ42Ўг45ЎдЈ¬ФтЎП1өДУаҪЗөИУЪЈЁЎЎЎЎЈ©
A.47Ўг55ЎдB.47Ўг15ЎдC.48Ўг15ЎдD.137Ўг55Ўд
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘa+1КЗ4өДЛгКхЖҪ·ҪёщЈ¬b-1КЗ27өДБў·ҪёщЈ¬»ҜјтЗуЦөЈә2ЈЁ2a-b2Ј©-ЈЁ4a-a2Ј©.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪЎчABCЦРЈ¬ТФBCОӘЦұҫ¶өДФІ·ЦұрҪ»ұЯACЎўABУЪDЎўEБҪөгЈ¬Б¬ҪУBDЎўDEЈ®ИфBDЖҪ·ЦЎПABCЈ¬ФтПВБРҪбВЫІ»Т»¶ЁіЙБўөДКЗЈЁЎЎЎЎЈ©
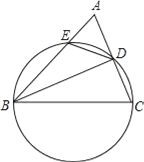
A. BDЎНAC B. AC2=2ABAE C. ЎчADEКЗөИСьИэҪЗРО D. BC=2AD
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЙиx1Ј¬x2КЗТ»ФӘ¶юҙО·ҪіМax2+bx+c=0ЈЁaЎЩ0Ј©өДБҪёщЈ¬
ЈЁ1Ј©КФНЖөјx1+x2=-![]() Ј¬x1ЎӨx2=
Ј¬x1ЎӨx2=![]() Ј»
Ј»
ЈЁ2Ј©ЗуҙъКэКҪaЈЁx13+x23Ј©+bЈЁx12+x22Ј©+cЈЁx1+x2Ј©өДЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
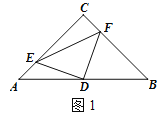
ЎҫМвДҝЎҝИзНјЈ¬ЎчABCЦРЈ¬AC=BCЈ¬ЎПC=90ЎгЈ¬өгDКЗABөДЦРөг.
ЈЁ1Ј©ИзНј1Ј¬ИфөгEЎўF·ЦұрКЗACЎўBCЙПөДөгЈ¬ЗТAE=CFЈ¬ЗлЕРұрЎчDEFөДРОЧҙЈ¬ІўЛөГчАнУЙЈ»
ЈЁ2Ј©ИфөгEЎўF·ЦұрКЗCAЎўBCСУіӨПЯЙПөДөгЈ¬ЗТAE=CFЈ¬ФтЈЁ1Ј©ЦРөДҪбВЫКЗ·сИФИ»іЙБўЈҝЗл
ЛөГчАнУЙ.
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com