
【题目】如图, ⊙O 的半径是2,直线l与⊙O 相交于A、B 两点,M、N 是⊙O 上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB 面积的最大值是 .

【答案】4![]()
【解析】试题分析:过点O作OC⊥AB于C,交⊙O于D、E两点,连结OA、OB、DA、DB、EA、EB,根据圆周角定理得∠AOB=2∠AMB=90°,则△OAB为等腰直角三角形,所以AB=![]() OA=2
OA=2![]() ,由于S四边形MANB=S△MAB+S△NAB,而当M点到AB的距离最大,△MAB的面积最大;当N点到AB的距离最大时,△NAB的面积最大,即M点运动到D点,N点运动到E点,所以四边形MANB面积的最大值=S四边形DAEB=S△DAB+S△EAB=
,由于S四边形MANB=S△MAB+S△NAB,而当M点到AB的距离最大,△MAB的面积最大;当N点到AB的距离最大时,△NAB的面积最大,即M点运动到D点,N点运动到E点,所以四边形MANB面积的最大值=S四边形DAEB=S△DAB+S△EAB=![]() ABCD+
ABCD+![]() ABCE=
ABCE=![]() AB(CD+CE)=
AB(CD+CE)=![]() ABDE=
ABDE=![]() ×2
×2![]() ×4=4
×4=4![]() .
.
试题解析:过点O作OC⊥AB于C,交⊙O于D、E两点,连结OA、OB、DA、DB、EA、EB,如图,
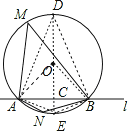
∵∠AMB=45°,
∴∠AOB=2∠AMB=90°,
∴△OAB为等腰直角三角形,
∴AB=![]() OA=2
OA=2![]() ,
,
∵S四边形MANB=S△MAB+S△NAB,
∴当M点到AB的距离最大,△MAB的面积最大;当N点到AB的距离最大时,△NAB的面积最大,
即M点运动到D点,N点运动到E点,
此时四边形MANB面积的最大值= S四边形DAEB=S△DAB+S△EAB=![]() ABCD+
ABCD+![]() ABCE=
ABCE=![]() AB(CD+CE)=
AB(CD+CE)=![]() ABDE=
ABDE=![]() ×2
×2![]() ×4=4
×4=4![]() .
.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料:对于平面图形A,如果存在一个圆,使图形A上的任意一点到圆心的距离都不大于这个圆的半径,则称图形A被这个圆所覆盖.回答下列问题:
(1)边长为1cm的正方形被一个半径为r的圆所覆盖,r的最小值是______ cm;
(2)边长为1cm的等边三角形被一个半径为r的圆所覆盖,r的最小值是______ cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
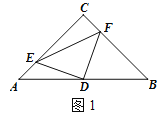
【题目】如图,△ABC中,AC=BC,∠C=90°,点D是AB的中点.
(1)如图1,若点E、F分别是AC、BC上的点,且AE=CF,请判别△DEF的形状,并说明理由;
(2)若点E、F分别是CA、BC延长线上的点,且AE=CF,则(1)中的结论是否仍然成立?请
说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中不正确的是( )
A. 抛掷一枚硬币,硬币落地时正面朝上是随机事件
B. 把4个球放入三个抽屉中,其中一个抽屉中至少有2个球是必然事件
C. 任意打开七年级下册数学教科书,正好是97页是确定事件
D. 一个盒子中有白球m个,红球6个,黑球n个(每个除了颜色外都相同).如果从中任取一个球,取得的是红球的概率与不是红球的概率相同,那么m与n的和是6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了保护环境,某企业决定购买10台污水处理设备;现有A、B两种型号的设备,其中每台的价格、月处理污水量及年消耗费如下表:
A型 | B型 | |
价格(万元/台) | 12 | 10 |
处理污水量(吨/月) | 240 | 200 |
年消耗费(万元/台) | 1 | 1 |
经预算,该企业购买设备的资金不高于105万元。
(1) 请你设计该企业有几种购买方案;
(2)若该企业每月产生的污水量为2040吨,为了节约资金,应选择哪种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣a2)3+(﹣a3)2﹣a2a3;
(2)(3+a)(3﹣a)+a2;
(3)(x+y﹣3)(x+y+3);
(4)(![]() )﹣2+(﹣2)3+|﹣3|﹣(π﹣3.14)0.
)﹣2+(﹣2)3+|﹣3|﹣(π﹣3.14)0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com