考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:(1)可证∠BAE=∠DAC,可得△ACD≌△AEB;
(2)可证∠ABF=∠ADG,可得△ABF≌△ADG;
(3)可证AF=AG,可得△ACG≌△AEF;
(4)可求得∠BOD=180°-∠ABD-∠ADB;
(5)连接FG,可证∠FAG=∠AFG=∠AGF,可得△AGF为等边三角形;
(6)根据∠AFG=∠ABD可判定FG∥BC.
解答:解:(1)∵△ABD,△AEC都是等边三角形
∴∠BAD=∠DAE=∠DAE=60°,
∴∠BAE=∠DAC,
在△ACD和△AEB中,
.
∴△ACD≌△AEB(SAS);
(2)∵△ACD≌△AEB,
∴∠ABF=∠ADG,
在△ABF和△ADG中,
,
∴△ABF≌△ADG(ASA),
(3)∵△ABF≌△ADG
∴AF=AG,
在△ACG和△AEF中,
,
∴△ACG≌△AEF(SAS),
(4)∵△ACD≌△AEB,
∴∠ABE=∠ADC
∴∠BOD=180°-∠BDC-∠DBO=180°-(∠BDA+∠CDA)-(∠ABD-∠ABE)
=180°-∠ABD-∠ADB=60°.
(5)连接FG,
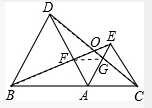
∵△ABF≌△ADG
∴AF=AG,
∵∠FAG=60°,
∴∠FAG=∠AFG=∠AGF,
∴△AFG为等边三角形.
(6)∵∠AFG=∠ABD,
∴FG∥BC.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角、对应边相等的性质,考查了等边三角形的性质.

 如图△ABD,△AEC都是等边三角形,求证:
如图△ABD,△AEC都是等边三角形,求证:


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案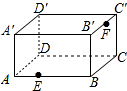 如图是放在地面上的一个长方体盒子,其中AB=9,BB′=5,B′C′=6,在线段AB的三等分点E(靠近点A)处有一只蚂蚁,B′C′中点F处有一米粒,则蚂蚁沿长方体表面爬到米粒处的最短距离为( )
如图是放在地面上的一个长方体盒子,其中AB=9,BB′=5,B′C′=6,在线段AB的三等分点E(靠近点A)处有一只蚂蚁,B′C′中点F处有一米粒,则蚂蚁沿长方体表面爬到米粒处的最短距离为( )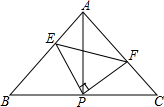 如图所示,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E,F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),给出以下五个结论:①AE=CF;②△EPF是等腰直角三角形;③S四边形AEPF=
如图所示,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E,F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),给出以下五个结论:①AE=CF;②△EPF是等腰直角三角形;③S四边形AEPF=