
ЁОЬтФПЁПвЛЬѕКгСїОЙ§![]() ЁЂ
ЁЂ![]() СНИіИлПкЃЌЫЎСїЕФЫйЖШЪЧ4ЧЇУз/ЪБЃЎМзЁЂввСНДЌЭЌЪБГіЗЂЃЌгЩ
СНИіИлПкЃЌЫЎСїЕФЫйЖШЪЧ4ЧЇУз/ЪБЃЎМзЁЂввСНДЌЭЌЪБГіЗЂЃЌгЩ![]() ИлПкЫГСїЪЛЯђ
ИлПкЫГСїЪЛЯђ![]() ИлПкЃЌМзДЌЕФОВЫЎЫйЖШПьгкввДЌЕФОВЫЎЫйЖШЃЎСНДЌЗжБ№ЕНДя
ИлПкЃЌМзДЌЕФОВЫЎЫйЖШПьгкввДЌЕФОВЫЎЫйЖШЃЎСНДЌЗжБ№ЕНДя![]() ИлПкКѓСЂМДЗЕЛи
ИлПкКѓСЂМДЗЕЛи![]() ИлПкЃЎСНДЌгы
ИлПкЃЎСНДЌгы![]() ИлПкЕФОрРы
ИлПкЕФОрРы![]() ЃЈЧЇУзЃЉгыГіЗЂЪБМф
ЃЈЧЇУзЃЉгыГіЗЂЪБМф![]() ЃЈЪБЃЉжЎМфЕФКЏЪ§ЭМЯёШчЭМЫљЪОЃЎ
ЃЈЪБЃЉжЎМфЕФКЏЪ§ЭМЯёШчЭМЫљЪОЃЎ
ЃЈ1ЃЉ![]() ЁЂ
ЁЂ![]() СНИлПкЯрОр ЧЇУзЃЎввДЌдкОВЫЎжаЕФЫйЖШЮЊ ЧЇУз/ЪБЃЎ
СНИлПкЯрОр ЧЇУзЃЎввДЌдкОВЫЎжаЕФЫйЖШЮЊ ЧЇУз/ЪБЃЎ
ЃЈ2ЃЉЧѓМзДЌДг![]() ИлПкЗЕЛи
ИлПкЗЕЛи![]() ИлПкЪБ
ИлПкЪБ![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЈ3ЃЉЧѓСНДЌдкЭОжаЯргіЪБЃЌЯргіДІгк![]() ИлПкжЎМфЕФОрРыЃЎ
ИлПкжЎМфЕФОрРыЃЎ
ЁОД№АИЁПЃЈ1ЃЉ96ЃЌ20ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ12ЧЇУз
ЃЛЃЈ3ЃЉ12ЧЇУз
ЁОНтЮіЁП
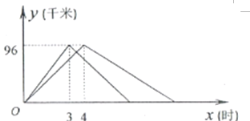
(1)ИљОнЭМЯѓМДПЩЕУГіAЁЂBСНИлПкЯрОр96ЧЇУзЃЛИљОнввДЌгЩAИлПкЫГСїЪЛЯђBИлПкгУСЫ4аЁЪБСаГіЗНГЬМДПЩЧѓЕУввДЌдкОВЫЎжаЕФЫйЖШЃЛ
(2)ИљОнМзДЌЯђAИлПкЫГСїЪЛЯђBИлПкЪБ3аЁЪБПЩЕУГіМзДЌФцЫЎЫйЖШЃЌНјЖјЕУГіМзДЌДгBИлПкЗЕЛиAИлПкЪБyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
(3)ИљОнЃЈ2ЃЉЕФНсТлвдМАввДЌгЩAИлПкЫГСїЪЛЯђBИлПкЪБyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНСаЗНГЬМДПЩНтД№ЃЎ
НтЃК(1)гЩЭМЯѓПЩжЊЃЌAЁЂBСНИлПкЯрОр96ЧЇУзЃЌ
ЩшввДЌдкОВЫЎжаЕФЫйЖШЮЊxЧЇУз/ЪБ
4ЁСЃЈx+4ЃЉ=96,
НтЕУx=20ЃЌ
МДввДЌдкОВЫЎжаЕФЫйЖШЮЊ20ЧЇУз/ЪБЃЌ
(2)МзДЌдкЫГЫЎЕФЫйЖШЮЊЃК![]() ЃЈЧЇУз/ЪБЃЉЃЌ
ЃЈЧЇУз/ЪБЃЉЃЌ
ЁрМзДЌФцЫЎЫйЖШЮЊЃК32-8=24ЃЈЧЇУз/ЪБЃЉЃЌ
Ёр![]() ЃЎ
ЃЎ
МДМзДЌДгBИлПкЗЕЛиAИлПкЪБyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЮЊЃК![]() ЃЎ
ЃЎ
(3)ИљОнЬтвтЕУЃК![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
![]() СНДЌдкЭОжаЯргіЪБЃЌЯргіДІгк
СНДЌдкЭОжаЯргіЪБЃЌЯргіДІгк![]() ИлПкЯрОр12ЧЇУзЃЎ
ИлПкЯрОр12ЧЇУзЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
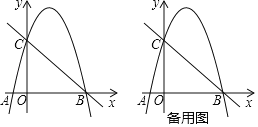
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§yЃНax2Љ3ax+cЕФЭМЯѓгыxжсНЛгкЕуAЁЂBЃЌгыyжсНЛгкЕуCжБЯпyЃНЉx+4ОЙ§ЕуBЁЂCЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉЙ§ЕуAЕФжБЯпНЛХзЮяЯпгкЕуMЃЌНЛжБЯпBCгкЕуNЃЎ
ЂйЕуNЮЛгкxжсЩЯЗНЪБЃЌЪЧЗёДцдкетбљЕФЕуMЃЌЪЙЕУAMЃКNMЃН5ЃК3ЃПШєДцдкЃЌЧѓГіЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЂкСЌНгACЃЌЕБжБЯпAMгыжБЯпBCЕФМаНЧЁЯANBЕШгкЁЯACBЕФ2БЖЪБЃЌЧыЧѓГіЕуMЕФКсзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
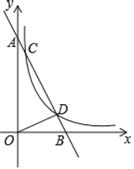
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯпABгыxжсНЛгкЕуBЃЌгыyжсНЛгкЕуAЃЌжБЯпABгыЗДБШР§КЏЪ§yЃН![]() ЃЈmЃО0ЃЉдкЕквЛЯѓЯоЕФЭМЯѓНЛгкЕуCЁЂЕуDЃЌЦфжаЕуCЕФзјБъЮЊЃЈ1ЃЌ8ЃЉЃЌЕуDЕФзјБъЮЊЃЈ4ЃЌnЃЉЃЎ
ЃЈmЃО0ЃЉдкЕквЛЯѓЯоЕФЭМЯѓНЛгкЕуCЁЂЕуDЃЌЦфжаЕуCЕФзјБъЮЊЃЈ1ЃЌ8ЃЉЃЌЕуDЕФзјБъЮЊЃЈ4ЃЌnЃЉЃЎ
ЃЈ1ЃЉЗжБ№ЧѓmЁЂnЕФжЕЃЛ
ЃЈ2ЃЉСЌНгODЃЌЧѓЁїADOЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌСтаЮABCDЕФБпADЁЭyжсЃЌДЙзуЮЊЕуEЃЌЖЅЕуAдкЕкЖўЯѓЯоЃЌЖЅЕуBдкyжсЕФе§АыжсЩЯЃЌЗДБШР§КЏЪ§yЃН![]() (kЁй0ЃЌxЃО0)ЕФЭМЯѓОЙ§ЖЅЕуCЁЂDЃЌШєЕуCЕФКсзјБъЮЊ5ЃЌBEЃН3DEЃЌдђkЕФжЕЮЊ______ЃЎ
(kЁй0ЃЌxЃО0)ЕФЭМЯѓОЙ§ЖЅЕуCЁЂDЃЌШєЕуCЕФКсзјБъЮЊ5ЃЌBEЃН3DEЃЌдђkЕФжЕЮЊ______ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
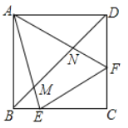
ЁОЬтФПЁПЃЈ1ЃЉШчЭМЂйЃЌЫФБпаЮ ABCD ЪЧе§ЗНаЮЃЌЕу G ЪЧ BC ЩЯЕФШЮвтвЛЕуЃЌBF AG гкЕу FЃЌDE AGгкЕу EЃЌЬНОП BFЃЌDEЃЌEF жЎМфЕФЪ§СПЙиЯЕЃЎЕквЛбЇЯАаЁзщКЯзїЬНОПКѓЃЌЕУЕНDEЈCBF= EFЃЌЧыжЄУїетИіНсТлЃЛ
ЃЈ2ЃЉШєЃЈ1ЃЉжаЕФЕу G дк CB ЕФбгГЄЯпЩЯЃЌЦфгрЬѕМўВЛБфЃЌЧыдкЭМЂкжаЛГіЭМаЮЃЌВЂжБНгаДГіДЫЪБ BFЃЌDEЃЌEF жЎМфЕФЪ§СПЙиЯЕЃЛ
ЃЈ3ЃЉШчЭМ Ђл ЃЌЫФБпаЮ ABCD ФкНггк ЁбOЃЌAB=ADЃЌE ЃЌF ЪЧAC ЩЯЕФСНЕуЃЌЧвТњзуЁЯAED=ЁЯBFA=ЁЯBCDЃЎЪдХаЖЯ ACЃЌDEЃЌBF жЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНааЫФБпаЮABCDжаЃЌЖдНЧЯпACЃЌBDНЛгкЕуOЃЌEЪЧБпADЩЯЕФвЛИіЖЏЕу(гыЕуAЃЌDВЛжиКЯ)ЃЌСЌНгEOВЂбгГЄЃЌНЛBCгкЕуFЃЌСЌНгBEЃЌDFЃЎЯТСаЫЕЗЈ:
Ђй ЖдгкШЮвтЕФЕуEЃЌЫФБпаЮBEDFЖМЪЧЦНааЫФБпаЮ;
Ђк ЕБЁЯABC>90ЁуЪБЃЌжСЩйДцдквЛИіЕуEЃЌЪЙЕУЫФБпаЮBEDFЪЧОиаЮ;
Ђл ЕБAB<ADЪБЃЌжСЩйДцдквЛИіЕуEЃЌЪЙЕУЪЧЫФБпаЮBEDFЪЧСтаЮ;
Ђм ЕБЁЯADB=45ЁуЪБЃЌжСЩйДцдквЛИіЕуEЃЌЪЙЕУЪЧЫФБпаЮBEDFЪЧе§ЗНаЮЃЎ
Ыљгае§ШЗЫЕЗЈЕФађКХЪЧЃК_________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋДг1ПЊЪМЕФСЌајздШЛЪ§АДЭМЙцТЩХХСаЃК
Са аа | Ек1Са | Ек2Са | Ек3Са | Ек4Са |
Ек1аа | 1 | 2 | 3 | 4 |
Ек2аа | 8 | 7 | 6 | 5 |
Ек3аа | 9 | 10 | 11 | 12 |
Ек4аа | 16 | 15 | 14 | 13 |
Ё | Ё | Ё | Ё | Ё |
Ек | Ё | Ё | Ё | Ё |
ЙцЖЈЮЛгкЕк![]() ааЃЌЕк
ааЃЌЕк![]() СаЕФздШЛЪ§10МЧЮЊ
СаЕФздШЛЪ§10МЧЮЊ![]() ЃЌздШЛЪ§15МЧЮЊ
ЃЌздШЛЪ§15МЧЮЊ![]() ЁАДДЫЙцТЩЃЌздШЛЪ§2018МЧЮЊ______ЃЎ
ЁАДДЫЙцТЩЃЌздШЛЪ§2018МЧЮЊ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮ![]() жаЃЌЕу
жаЃЌЕу![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() БпЩЯЕФСНЕуЃЌЧв
БпЩЯЕФСНЕуЃЌЧв![]() ЗжБ№НЛ
ЗжБ№НЛ![]() гк
гк![]() .ЯТСаНсТлЃКЂй
.ЯТСаНсТлЃКЂй![]() ЃЛЂк
ЃЛЂк![]() ЦНЗж
ЦНЗж![]() ЃЛЂл
ЃЛЂл![]() ЃЛЂм
ЃЛЂм![]()
![]() ЃЎЦфжае§ШЗЕФНсТлЪЧЃЈ ЃЉ
ЃЎЦфжае§ШЗЕФНсТлЪЧЃЈ ЃЉ
A.ЂкЂлЂмB.ЂйЂмC.ЂйЂкЂлD.ЂйЂкЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌЕуCЪЧЯпЖЮABЩЯвЛЕуЃЌACЃН![]() ABЃЌBCЮЊЁбOЕФжБОЖЃЎ
ABЃЌBCЮЊЁбOЕФжБОЖЃЎ
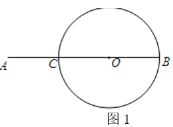
ЃЈ1ЃЉдкЭМ1жБОЖBCЩЯЗНЕФдВЛЁЩЯеввЛЕуPЃЌЪЙЕУPAЃНPBЃЛЃЈгУГпЙцзїЭМЃЌБЃСєзїЭМКлМЃЃЌВЛвЊЧѓаДзїЗЈЃЉ
ЃЈ2ЃЉСЌНгPAЃЌЧѓжЄЃКPAЪЧЁбOЕФЧаЯпЃЛ
ЃЈ3ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌСЌНгPCЁЂPBЃЌЁЯPABЕФЦНЗжЯпЗжБ№НЛPCЁЂPBгкЕуDЁЂEЃЎЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com