
【题目】如图,在正方形![]() 中,点
中,点![]() 分别是
分别是![]() 边上的两点,且
边上的两点,且![]() 分别交
分别交![]() 于
于![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() 平分
平分![]() ;③
;③![]() ;④
;④![]()
![]() .其中正确的结论是( )
.其中正确的结论是( )
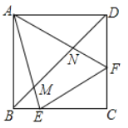
A.②③④B.①④C.①②③D.①②③④
【答案】D
【解析】
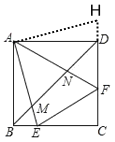
把△ABE绕点A逆时针旋转90°,得到△ADH,证明△AEF≌△AHF,利用全等三角形的性质可得①②正确;求出∠BAN=∠AMD,根据∠ABN=∠ADM=45°,证明△ABN∽△MDA,利用相似三角形的性质可得④正确;求出∠AFE=∠AMN,证明△AMN∽△AFE,利用相似三角形的性质可得③正确.
解:如图,把△ABE绕点A逆时针旋转90°,得到△ADH,易得H、D、F三点共线,
∵∠BAD=90°,∠EAF=45°,
∴∠BAE+∠DAF=45°,
∴∠DAH+∠DAF=45°,
∴∠EAF=∠HAF,
∵AE=AH,AF=AF,
∴△AEF≌△AHF,
∴EF=FH,∠AFH=∠AFE,
∴EF=FH=DH+DF=BE+DF,AF平分∠DFE,故①②正确;
∵∠BAN=∠BAM+∠MAN=∠BAM+45°,∠AMD=∠ABM+∠BAM=45°+∠BAM,
∴∠BAN=∠AMD,
∵∠ABN=∠ADM=45°,
∴△ABN∽△MDA,
∴![]() ,
,
∵AD=AB,
∴AB2=BNDM,故④正确;
∵AB∥CD,
∴∠DFA=∠BAN,
∵∠AFE=∠AFD,∠BAN=∠AMD,
∴∠AFE=∠AMN,
又∵∠MAN=∠FAE,
∴△AMN∽△AFE,
∴![]() ,即AMAE=ANAF,故③正确,
,即AMAE=ANAF,故③正确,
故选:D.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
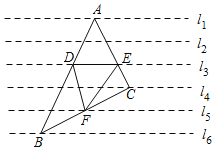
【题目】如图,一组等距的平行线,点A、B、C分别在直线l1、l6、l4上,AB交l3于点D,AC交l3于点E,BC交于l5点F,若△DEF的面积为1,则△ABC的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一条河流经过![]() 、
、![]() 两个港口,水流的速度是4千米/时.甲、乙两船同时出发,由
两个港口,水流的速度是4千米/时.甲、乙两船同时出发,由![]() 港口顺流驶向
港口顺流驶向![]() 港口,甲船的静水速度快于乙船的静水速度.两船分别到达
港口,甲船的静水速度快于乙船的静水速度.两船分别到达![]() 港口后立即返回
港口后立即返回![]() 港口.两船与
港口.两船与![]() 港口的距离
港口的距离![]() (千米)与出发时间
(千米)与出发时间![]() (时)之间的函数图像如图所示.
(时)之间的函数图像如图所示.
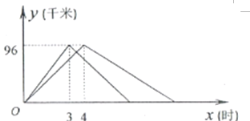
(1)![]() 、
、![]() 两港口相距 千米.乙船在静水中的速度为 千米/时.
两港口相距 千米.乙船在静水中的速度为 千米/时.
(2)求甲船从![]() 港口返回
港口返回![]() 港口时
港口时![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(3)求两船在途中相遇时,相遇处于![]() 港口之间的距离.
港口之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
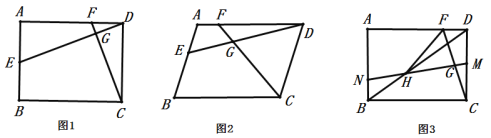
【题目】菱形![]() 中,
中,![]() 为边
为边![]() 上的点,
上的点,![]() 相交于点
相交于点![]() .
.
(1)如图1,若![]() ,
,![]() ,求证:
,求证:![]() ;
;
(2)如图2,若![]() .求证:
.求证:![]() ;
;
(3)如图3,在(1)的条件下,平移线段![]() 到
到![]() ,使
,使![]() 为
为![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,请直接写出
,请直接写出![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
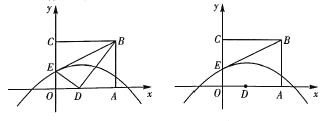
【题目】如图,若折叠矩形![]() 的一边
的一边![]() ,使点
,使点![]() 落在
落在![]() 边的点
边的点![]() 处,已知折痕
处,已知折痕![]() 且.以
且.以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴建立如图所示的平面直角坐标系,抛物线
轴建立如图所示的平面直角坐标系,抛物线![]() 经过点
经过点![]() .
.
(1)求![]() 的值;
的值;
(2)点![]() 是线段
是线段![]() 上一动点,点
上一动点,点![]() 在抛物线上,且始终满足
在抛物线上,且始终满足![]() ,在点
,在点![]() 运动过程中,能否使得
运动过程中,能否使得![]() ?若能,求出所有符合条件的点
?若能,求出所有符合条件的点![]() 的坐标;若不能,请说明理由;
的坐标;若不能,请说明理由;
(3)已知点![]() 是拋物线上一动点,点
是拋物线上一动点,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,若在
,若在![]() 轴上存在一点
轴上存在一点![]() ,使
,使![]() 有最小值,求点
有最小值,求点![]() 的纵坐标的最大值.
的纵坐标的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设等边三角形的内切圆半径为![]() 外接圆半径为
外接圆半径为![]() ,平面内任意一点
,平面内任意一点![]() 到等边三角形中心的距离为
到等边三角形中心的距离为![]() 若满足
若满足![]() 则称点
则称点![]() 叫做等边三角形的中心关联点.在平面直角坐标系
叫做等边三角形的中心关联点.在平面直角坐标系![]() 中,等边
中,等边![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() .
.
(1)①等边![]() 中心的坐标为 ;
中心的坐标为 ;
②已知点![]() 在
在![]() 中,是等边
中,是等边![]() 的中心关联点的是 ;
的中心关联点的是 ;
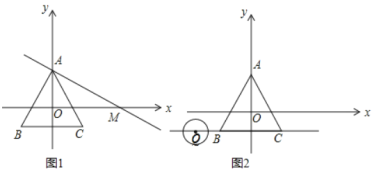
(2)如图1,过点![]() 作直线交
作直线交![]() 轴正半轴于
轴正半轴于![]() 使
使![]() .
.
①若线段![]() 上存在等边
上存在等边![]() 的中心关联点
的中心关联点![]() 求
求![]() 的取值范围;
的取值范围;
②将直线![]() 向下平移得到直线
向下平移得到直线![]() 当
当![]() 满足什么条件时,直线
满足什么条件时,直线![]() 上总存在等边
上总存在等边![]() 的中心关联点;
的中心关联点;
(3)如图2,点![]() 为直线
为直线![]() 上一动点,
上一动点,![]() 的半径为
的半径为![]() 当
当![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度向右移动,运动时间为
个单位的速度向右移动,运动时间为![]() 秒.是否存在某一时刻
秒.是否存在某一时刻![]() 使得
使得![]() 上所有点都是等边
上所有点都是等边![]() 的中心关联点?如果存在,请直接写出所有符合题意的
的中心关联点?如果存在,请直接写出所有符合题意的![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
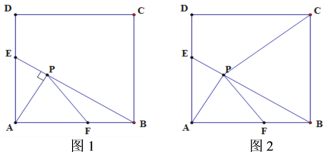
【题目】如图,边长为6的正方形ABCD中,E,F分别是AD,AB上的点,AP⊥BE,P为垂足.
(1)如图1,AF=BF,AE=![]() ,点T是射线PF上的一个动点,当△ABT为直角三角形时,求AT的长;
,点T是射线PF上的一个动点,当△ABT为直角三角形时,求AT的长;
(2)如图2,若AE=AF,连接CP,求证:CP⊥FP.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】家庭过期药品属于“危险废物”,处理不当将污染环境,危害健康某市药监部门为了解家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调查.
(1)下列选取样本的方法最合理的一种是 (只需填上正确答案的序号)
①在市中心某个居民区以家庭为单位随机抽取;
②在全市医务工作者中以家庭为单位随机抽取;
③在全市常住人口中以家庭为单位随机抽取.
(2)本次抽样调查发现,接受调查的家庭都有过期药品,现将有关数据呈现如下图:
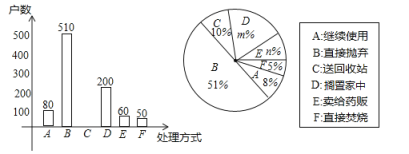
①![]() ,
,
②补全条形统计图;(标上数据)
③家庭过期药品的正确处理方式是送回收站,若该市有![]() 万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收站.
万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收站.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+![]() .其中正确结论的序号是( )
.其中正确结论的序号是( )

A.①③④ B.①②⑤ C.③④⑤ D.①③⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com