
【题目】设等边三角形的内切圆半径为![]() 外接圆半径为
外接圆半径为![]() ,平面内任意一点
,平面内任意一点![]() 到等边三角形中心的距离为
到等边三角形中心的距离为![]() 若满足
若满足![]() 则称点
则称点![]() 叫做等边三角形的中心关联点.在平面直角坐标系
叫做等边三角形的中心关联点.在平面直角坐标系![]() 中,等边
中,等边![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() .
.
(1)①等边![]() 中心的坐标为 ;
中心的坐标为 ;
②已知点![]() 在
在![]() 中,是等边
中,是等边![]() 的中心关联点的是 ;
的中心关联点的是 ;
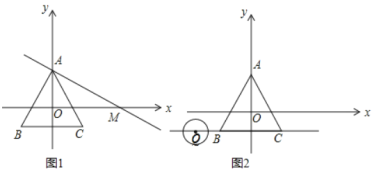
(2)如图1,过点![]() 作直线交
作直线交![]() 轴正半轴于
轴正半轴于![]() 使
使![]() .
.
①若线段![]() 上存在等边
上存在等边![]() 的中心关联点
的中心关联点![]() 求
求![]() 的取值范围;
的取值范围;
②将直线![]() 向下平移得到直线
向下平移得到直线![]() 当
当![]() 满足什么条件时,直线
满足什么条件时,直线![]() 上总存在等边
上总存在等边![]() 的中心关联点;
的中心关联点;
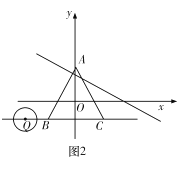
(3)如图2,点![]() 为直线
为直线![]() 上一动点,
上一动点,![]() 的半径为
的半径为![]() 当
当![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度向右移动,运动时间为
个单位的速度向右移动,运动时间为![]() 秒.是否存在某一时刻
秒.是否存在某一时刻![]() 使得
使得![]() 上所有点都是等边
上所有点都是等边![]() 的中心关联点?如果存在,请直接写出所有符合题意的
的中心关联点?如果存在,请直接写出所有符合题意的![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
【答案】(1)①![]() ;②
;②![]() ;(2)①
;(2)①![]() ,②满足条件的
,②满足条件的![]() 的值为
的值为![]() ;(3)存在.
;(3)存在. ![]() 或
或![]() .
.
【解析】
(1)①求出OA=OB=OC=2,即可得等边![]() 中心的坐标;
中心的坐标;
②分别求出OD,OE,OF,然后根据中心关联点的定义判断;
(2)①易得直线![]() 的解析式,判断出点
的解析式,判断出点![]() 在直线AM上,根据点P在AE上时
在直线AM上,根据点P在AE上时![]() ,可得此时点P都是等边△ABC的中心关联点;
,可得此时点P都是等边△ABC的中心关联点;
②如图1-2中,设平移后的直线交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作这条直线的垂线,垂足为
作这条直线的垂线,垂足为![]() ,求出
,求出![]() 时OG的长,即可得到b的取值范围;
时OG的长,即可得到b的取值范围;
(3)如图2中,设Q(s,1),由题意得当OQ=![]() 时,⊙Q上所有点都是等边△ABC的中心关联点,求出s即可得解.
时,⊙Q上所有点都是等边△ABC的中心关联点,求出s即可得解.
解:(1)①∵![]() ,
,
∴OA=2,OB=![]() ,OC=
,OC=![]() ,
,
∴等边![]() 中心的坐标为
中心的坐标为![]() ;
;
②由题意得:![]() ,点
,点![]() 是
是![]() 的中心,
的中心,
![]() ,
,
![]() 点
点![]() 是
是![]() 的中心关联点;
的中心关联点;
(2)①如图1-1中,
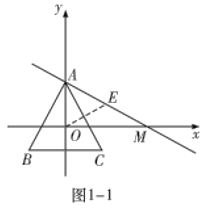
∵OA=2,![]() ,
,
∴OM=![]() ,
,
易得直线![]() 的解析式为:
的解析式为:![]() ,
,
∴![]() 在直线
在直线![]() 上,
上,
因为![]()
![]() ,
,
所以![]() 为等边三角形,
为等边三角形,
所以![]() 边上的高长为
边上的高长为![]() ,
,
当点![]() 在
在![]() 上时,
上时,![]() ,
,
所以当点![]() 在
在![]() 上时,点
上时,点![]() 都是等边
都是等边![]() 的中心关联点,
的中心关联点,
所以![]() ;
;
![]() 如图1-2中,设平移后的直线交
如图1-2中,设平移后的直线交![]() 轴于点
轴于点![]() 过点
过点![]() 作这条直线的垂线,垂足为
作这条直线的垂线,垂足为![]() ,
,
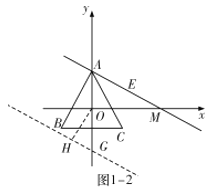
当![]() 时,在
时,在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() 满足条件的
满足条件的![]() 的值为
的值为![]() ;
;
![]() 存在,
存在,
理由:如图2中,设![]() ,
,
由题意得,当![]() 时,
时,![]() 上所有点都是等边
上所有点都是等边![]() 的中心关联点,
的中心关联点,
∴![]() ,
,
解得:![]() ,
,
![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A、B、C三点的坐标分别为:A(1,4)、B(0,3)、C(3,0),若P为x轴上一点,且∠BPC=2∠ACB,则点P的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,对角线AC,BD交于点O,E是边AD上的一个动点(与点A,D不重合),连接EO并延长,交BC于点F,连接BE,DF.下列说法:
① 对于任意的点E,四边形BEDF都是平行四边形;
② 当∠ABC>90°时,至少存在一个点E,使得四边形BEDF是矩形;
③ 当AB<AD时,至少存在一个点E,使得是四边形BEDF是菱形;
④ 当∠ADB=45°时,至少存在一个点E,使得是四边形BEDF是正方形.
所有正确说法的序号是:_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】再读教材:宽与长的比是![]() (约为0.618)的矩形叫作黄金矩形.黄金矩形给我们以协调、匀称的美感,世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计.下面,我们用宽为2的矩形纸片折叠黄金矩形(提示:
(约为0.618)的矩形叫作黄金矩形.黄金矩形给我们以协调、匀称的美感,世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计.下面,我们用宽为2的矩形纸片折叠黄金矩形(提示:![]() ).
).
第一步:在矩形纸片一端 ,利用图1的方法折出一个正方形,然后把纸片展平;
第二步:如图2,把这个正方形折成两个相等的矩形,再把纸片展平;
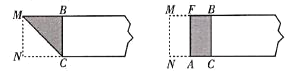
图1 图2
第三步:折出内侧矩形的对角线![]() ,并把
,并把![]() 折到图3中所示的
折到图3中所示的![]() 处;
处;
第四步:展平纸片,按照所得的点![]() 折出
折出![]() ,使
,使![]() ,则图4中就会出现黄金矩形.
,则图4中就会出现黄金矩形.
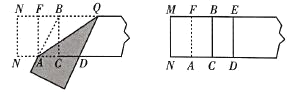
图3 图4
(1)在图3中![]() _________ (保留根号);
_________ (保留根号);
(2)如图3,则四边形![]() 的形状是_________;
的形状是_________;
(3)在图4中黄金矩形是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,点
中,点![]() 分别是
分别是![]() 边上的两点,且
边上的两点,且![]() 分别交
分别交![]() 于
于![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() 平分
平分![]() ;③
;③![]() ;④
;④![]()
![]() .其中正确的结论是( )
.其中正确的结论是( )
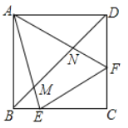
A.②③④B.①④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O直径,OE⊥BC垂足为E,AB⊥CD垂足为F.
(1)求证:AD=2OE;
(2)若∠ABC=30°,⊙O的半径为2,求两阴影部分面积的和.
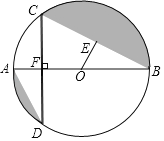
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2﹣2ax+c(a<0)的图象过点A(3,m).
(1)当a=﹣1,m=0时,求抛物线的顶点坐标_____;
(2)如图,直线l:y=kx+c(k<0)交抛物线于B,C两点,点Q(x,y)是抛物线上点B,C之间的一个动点,作QD⊥x轴交直线l于点D,作QE⊥y轴于点E,连接DE.设∠QED=β,当2≤x≤4时,β恰好满足30°≤β≤60°,a=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 与
与![]() 轴交于点C,与
轴交于点C,与![]() 轴的正半轴交于点K,过点
轴的正半轴交于点K,过点![]() 作
作![]() 轴交抛物线于另一点B,点
轴交抛物线于另一点B,点![]() 在
在![]() 轴的负半轴上,连结
轴的负半轴上,连结![]() 交
交![]() 轴于点A,若
轴于点A,若![]() .
.
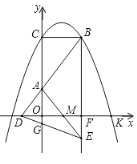
(1)用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(2)当![]() 时,判断点
时,判断点![]() 是否落在抛物线上,并说明理由;
是否落在抛物线上,并说明理由;
(3)过点![]() 作
作![]() 轴交
轴交![]() 轴于点
轴于点![]() 延长
延长![]() 至
至![]() ,使得
,使得![]() 连结
连结![]() 交
交![]() 轴于点
轴于点![]() 连结AE交
连结AE交![]() 轴于点
轴于点![]() 若
若![]() 的面积与
的面积与![]() 的面积之比为
的面积之比为![]() 则求出抛物线的解析式.
则求出抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年3月15日,我国“两会”落下帷幕.13天时间里,来自各地的5000余名代表、委员聚于国家政治中心,共议国家发展大计.某校初三(3)班张老师为了了解同学们对“两会”知识的知晓情况,进行了一次小测试,测试满分100分.其中
A组同学的测试成绩分别为:91 91 86 93 85 89 89 88 87 91
B组同学的测试成绩分别为:88 97 88 85 86 94 84 83 98 87
根据以上数据,回答下列问题:
(1)完成下表:
组别 | 平均数 | 中位数 | 众数 | 方差 |
A组 | 89 | 89 | b | c |
B组 | 89 | a | 88 | 26.2 |
其中a= ,b= ,c= ,
(2)张老师将B组同学的测试成绩分成四组并绘制成如图所示频数分布直方图(不完整),请补全;
(3)根据以上分析,你认为 组(填“A”或“B”)的同学对今年“两会”知识的知晓情况更好一些,请写出你这样判断的理由(至少写两条):① ② .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com