
����Ŀ���ٶ��̲ģ����볤�ı���![]() (ԼΪ0.618)�ľ��ν����ƽ���Σ��ƽ���θ�������Э�����ȳƵ����У�����������������Ľ�����Ϊȡ����ѵ��Ӿ�Ч�����������˻ƽ���ε���ƣ����棬�����ÿ�Ϊ2�ľ���ֽƬ�۵��ƽ����(��ʾ��
(ԼΪ0.618)�ľ��ν����ƽ���Σ��ƽ���θ�������Э�����ȳƵ����У�����������������Ľ�����Ϊȡ����ѵ��Ӿ�Ч�����������˻ƽ���ε���ƣ����棬�����ÿ�Ϊ2�ľ���ֽƬ�۵��ƽ����(��ʾ��![]() )��
)��
��һ�����ھ���ֽƬһ�� ������ͼ1�ķ����۳�һ�������Σ�Ȼ���ֽƬչƽ��
�ڶ�������ͼ2��������������۳�������ȵľ��Σ��ٰ�ֽƬչƽ��
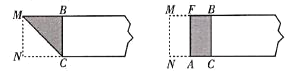
ͼ1 ͼ2
���������۳��ڲ���εĶԽ���![]() ������
������![]() �۵�ͼ3����ʾ��
�۵�ͼ3����ʾ��![]() ����
����
���IJ���չƽֽƬ���������õĵ�![]() �۳�
�۳�![]() ��ʹ
��ʹ![]() ����ͼ4�оͻ���ֻƽ���Σ�
����ͼ4�оͻ���ֻƽ���Σ�
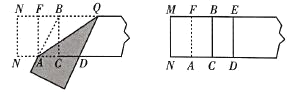
ͼ3 ͼ4
(1)��ͼ3��![]() _________ (��������)��
_________ (��������)��
(2)��ͼ3�����ı���![]() ����״��_________��
����״��_________��
(3)��ͼ4�лƽ������_________��
���𰸡�![]() ���� ����
���� ����![]() ������
������![]()
��������
��1�����ɶ��������AB�ij���
��2����֪BQ��AD����֤AB��QD֤�ı���BADQ��ƽ���ı��Σ������֤BA=AD�����Σ�
��3��Ѱ�ұ߳�Ϊ![]() ��2�ľ��Σ�������BCDE�ǻƽ�أ�������Ѱ��
��2�ľ��Σ�������BCDE�ǻƽ�أ�������Ѱ��![]() ��2�ľ��Σ�ʹ
��2�ľ��Σ�ʹ![]() Ϊ��ĸ����ĸ��������Ҳ�ɵõ�
Ϊ��ĸ����ĸ��������Ҳ�ɵõ�![]() ��������MNDE
��������MNDE
��1����MN=2����AC=1��BC=2
����Rt��BAC�У����ݹ��ɶ�����AB=![]()
��2�����ı���MNCB�������Σ���BQ��AD
���۳��ڲ���εĶԽ���![]() ������
������![]() �۵�ͼ3����ʾ��
�۵�ͼ3����ʾ��![]() ��
��
���BAQ=��QAD����BQA=��AQD��AB=AD
��BQ��AD�����BQA=��QAD�����BAQ=��AQD
��AB��QD�����ı���BADQ��ƽ���ı���
��AB=AD����ƽ���ı���BADQ������
��3�����ı���BADQ�����Σ���AD=AB=![]()
��AN=AC=1����CD=![]()
��BC=2����![]() �������BCDE�ǻƽ����
�������BCDE�ǻƽ����
��![]() �������MNDE�ǻƽ����
�������MNDE�ǻƽ����


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�Ҿ��̳��ƻ�����ij�ֲ��������ν������ۣ��й���Ϣ�����
ԭ���ۣ�Ԫ/�ţ� | ���ۼۣ�Ԫ/�ţ� | �����ۼۣ�Ԫ/�ף� | |
���� | a | 270 | 500Ԫ |
���� | a��110 | 70 |
��֪��600Ԫ�����IJ�����������160Ԫ�����IJ���������ͬ��
��1�������a��ֵ��
��2�������̳��������ε������Dz���������5������20�ţ��Ҳ����Ͳ��ε�������������200�ţ����̳��ƻ���һ��IJ������ף�һ�Ų��������Ų������һ�ף����ۣ�������������������۷�ʽ���ۣ������������������ܻ�����������������Ƕ��٣�
��3������ԭ���ϼ۸����ǣ�ÿ�Ų����Ͳ��εĽ��۶�������10Ԫ�������ۼ۸ֲ��䣮�̳������˲����Ͳ��ι�200�ţ�Ӧ�������ų������۵�������������10�����ϣ���ʹ��ʵ��ȫ���۳�����������루2������ͬ��������������������۷�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ܹ����⸴�Ӷ��ľ��û���Ӱ�죬ȥ��1��7�£�ԭ���ϼ۸�һ·��������ɳ��ij��װ��ÿ���·�ԭ���ϵijɱ�y1��Ԫ�����·�x��1��x��7����xΪ������֮��ĺ�����ϵ���±���
�·�x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
�ɱ���Ԫ/���� | 56 | 58 | 60 | 62 | 64 | 66 | 68 |
8��12�£����ž��û����ĺ�ת��ԭ���ϼ۸������������ÿ��ԭ���ϳɱ�y2��Ԫ�����·�x�ĺ�����ϵʽΪy2=x+62��8��x��12����xΪ��������
��1����۲�����е����ݣ���ѧ���ĺ������֪ʶ��y1��x�ĺ�����ϵʽ��
��2����ȥ����·�ÿ���ij�����Ϊ100Ԫ������ÿ���·��������ɱ�Ϊ8Ԫ�����·���1��7�µ�������p1����������·�x�����ϵʽp1=0.1x+1.1��1��x��7����xΪ�������� 8��12�µ�������p2����������·�x�����ϵʽp2=��0.1x+3��8��x��12����xΪ���������ó�ȥ���ĸ��������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,����ABCD�У�AD>AB������AC�����߶�AC�Ƶ�A˳ʱ����ת90�õ��߶�AE��ƽ���߶�AE�õ��߶�DF(��A���D��Ӧ����E���F��Ӧ)������BF���ֱ�ֱ��AD��AC�ڵ�G��M������EF��
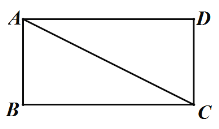
(1) �����ⲹȫͼ�Σ�
(2) ��֤��EG��AD��
(3) ����EC����BF�ڵ�N����AB=2��BC=4����MB=a��NF=b���ԱȽ�![]() ��
��![]() ֮��Ĵ�С��ϵ����֤����
֮��Ĵ�С��ϵ����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() �У�
�У�![]() Ϊ��
Ϊ��![]() �ϵĵ㣬
�ϵĵ㣬![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��
��1����ͼ1����![]() ��
��![]() ����֤��
����֤��![]() ��
��
��2����ͼ2����![]() ����֤��
����֤��![]() ��
��
��3����ͼ3���ڣ�1���������£�ƽ���߶�![]() ��
��![]() ��ʹ
��ʹ![]() Ϊ
Ϊ![]() ���е㣬����
���е㣬����![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ����ֱ��д��
����ֱ��д��![]() �ij��ȣ�
�ij��ȣ�
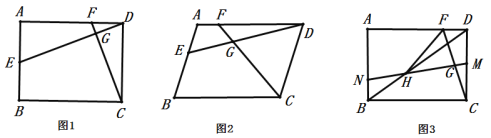
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��![]() �ڷ���������
�ڷ���������![]() ��ͼ���ϣ�����
��ͼ���ϣ�����![]() ��
��![]() �ᣬ����Ϊ
�ᣬ����Ϊ![]() ��ֱ��
��ֱ��![]() ������
������![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ��
��![]() .
.

��1����������![]() ��һ�κ���
��һ�κ���![]() �ı���ʽ��
�ı���ʽ��
��2��ֱ��д������![]() �IJ���ʽ
�IJ���ʽ![]() �Ľ⼯.
�Ľ⼯.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ȱ������ε�����Բ�뾶Ϊ![]() ���Բ�뾶Ϊ
���Բ�뾶Ϊ![]() ��ƽ��������һ��
��ƽ��������һ��![]() ���ȱ����������ĵľ���Ϊ
���ȱ����������ĵľ���Ϊ![]() ������
������![]() ��Ƶ�
��Ƶ�![]() �����ȱ������ε����Ĺ����㣮��ƽ��ֱ������ϵ
�����ȱ������ε����Ĺ����㣮��ƽ��ֱ������ϵ![]() �У��ȱ�
�У��ȱ�![]() ���������������ֱ�Ϊ
���������������ֱ�Ϊ![]() ��
��
��1���ٵȱ�![]() ���ĵ�����Ϊ ��
���ĵ�����Ϊ ��
����֪��![]() ��
��![]() �У��ǵȱ�
�У��ǵȱ�![]() �����Ĺ�������� ��
������������� ��
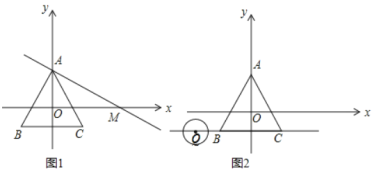
��2����ͼ1������![]() ��ֱ�߽�
��ֱ�߽�![]() ����������
����������![]() ʹ
ʹ![]() ��
��
����
�����߶�![]() �ϴ��ڵȱ�
�ϴ��ڵȱ�![]() �����Ĺ�����
����������![]() ��
��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�ڽ�ֱ��![]() ����ƽ�Ƶõ�ֱ��
����ƽ�Ƶõ�ֱ��![]() ��
��![]() ����ʲô����ʱ��ֱ��
����ʲô����ʱ��ֱ��![]() ���ܴ��ڵȱ�
���ܴ��ڵȱ�![]() �����Ĺ����㣻
�����Ĺ����㣻
��3����ͼ2����![]() Ϊֱ��
Ϊֱ��![]() ��һ���㣬
��һ���㣬![]() �İ뾶Ϊ
�İ뾶Ϊ![]() ��
��![]() �ӵ�
�ӵ�![]() ��������ÿ��
��������ÿ��![]() ����λ���ٶ������ƶ����˶�ʱ��Ϊ
����λ���ٶ������ƶ����˶�ʱ��Ϊ![]() �룮�Ƿ����ijһʱ��
�룮�Ƿ����ijһʱ��![]() ʹ��
ʹ��![]() �����е㶼�ǵȱ�
�����е㶼�ǵȱ�![]() �����Ĺ����㣿������ڣ���ֱ��д�����з��������
�����Ĺ����㣿������ڣ���ֱ��д�����з��������![]() ��ֵ����������ڣ���˵�����ɣ�
��ֵ����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ����ϣ���ʦ��ѧ��һ��ȥ����ѧУ����̨�����AB�ĸ߶ȣ���ͼ����ʦ�������̨ǰб��FC���±�ΪiFC=1��10����EF��CE=1��10����ѧ��С��վ��������̨ˮƽ����Ϊ35m����CE=35m������C�㣬�����˶���B������Ϊ������֪tan��=![]() ������̨��AF=1m��С������CD=1.6m�����С����������AB�ĸ߶ȣ�
������̨��AF=1m��С������CD=1.6m�����С����������AB�ĸ߶ȣ�
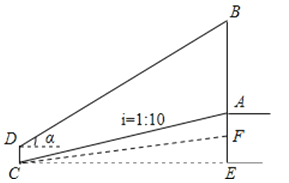
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�� ![]() ��ֱ��
��ֱ��![]() �ϵ����㣬ֱ��l1��l2�ij�ʼλ����ֱ��
�ϵ����㣬ֱ��l1��l2�ij�ʼλ����ֱ��![]() �غϽ�l1�Ƶ�
�غϽ�l1�Ƶ�![]() ˳ʱ����ÿ��10�����ٶ���ת����l2�Ƶ�B��ʱ����ÿ��5�����ٶ���ת��������ֱ�ߴ��غ�λ��ͬʱ��ʼ��ת������תʱ��Ϊ
˳ʱ����ÿ��10�����ٶ���ת����l2�Ƶ�B��ʱ����ÿ��5�����ٶ���ת��������ֱ�ߴ��غ�λ��ͬʱ��ʼ��ת������תʱ��Ϊ![]() ��(
��(![]() ��������)����
��������)����![]() ʱ����
ʱ����![]() �Ľ���Ϊ
�Ľ���Ϊ![]() ����
����![]() ʱ����
ʱ����![]() �Ľ���Ϊ
�Ľ���Ϊ![]() ����
����![]() ʱ��
ʱ��![]() �Ľ���Ϊ
�Ľ���Ϊ![]() ������ô��
������ô��![]() ʱ��
ʱ�� ![]() �ཻ���õĶ۽���__________����
�ཻ���õĶ۽���__________����![]() ����
����![]() �Ϸ�ʱ��
�Ϸ�ʱ�� ![]() ����Сֵ��__________��
����Сֵ��__________��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com