
【题目】受国内外复杂多变的经济环境影响,去年1至7月,原材料价格一路攀升,长沙市某服装厂每件衣服原材料的成本y1(元)与月份x(1≤x≤7,且x为整数)之间的函数关系如下表:
月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
成本(元/件) | 56 | 58 | 60 | 62 | 64 | 66 | 68 |
8至12月,随着经济环境的好转,原材料价格的涨势趋缓,每件原材料成本y2(元)与月份x的函数关系式为y2=x+62(8≤x≤12,且x为整数).
(1)请观察表格中的数据,用学过的函数相关知识求y1与x的函数关系式.
(2)若去年该衣服每件的出厂价为100元,生产每件衣服的其他成本为8元,该衣服在1至7月的销售量p1(万件)与月份x满足关系式p1=0.1x+1.1(1≤x≤7,且x为整数); 8至12月的销售量p2(万件)与月份x满足关系式p2=﹣0.1x+3(8≤x≤12,且x为整数),该厂去年哪个月利润最大;并求出最大利润.
【答案】(1)![]() (1≤x≤7,且x为整数);(2)该厂去年8月利润最大,最大利润为48.4万元.
(1≤x≤7,且x为整数);(2)该厂去年8月利润最大,最大利润为48.4万元.
【解析】
(1)由表格中数据可猜测,y1是x的一次函数.把表格(1)中任意两组数据代入直线解析式可得y1的解析式.
(2)分情况探讨得:1≤x≤7时,利润=P1×(售价﹣各种成本);80≤x≤12时,利润=P2×(售价﹣各种成本);并求得相应的最大利润即解.
解::(1)由表格中数据可猜测,y1是x的一次函数.
设![]()
则![]()
解得:![]()
∴![]() ,
,
经检验其它各点都符合该解析式,
∴![]() (1≤x≤7,且x为整数).
(1≤x≤7,且x为整数).
(2)设去年第x月的利润为w万元.
当1≤x≤7,且x为整数时,
![]()
![]()
![]()
![]()
∴当x=4时,w最大=45万元;
当8≤x≤12,且x为整数时,
![]()
![]()
![]()
![]()
∴当x=8时,w最大=48.4万元
∴该厂去年8月利润最大,最大利润为48.4万元.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A、B、C三点的坐标分别为:A(1,4)、B(0,3)、C(3,0),若P为x轴上一点,且∠BPC=2∠ACB,则点P的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
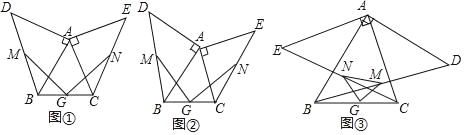
【题目】(1)操作发现:如图①,小明画了一个等腰三角形ABC,其中AB=AC,在△ABC的外侧分别以AB,AC为腰作了两个等腰直角三角形ABD,ACE,分别取BD,CE,BC的中点M,N,G,连接GM,GN.小明发现了:线段GM与GN的数量关系是__________;位置关系是__________.
(2)类比思考:
如图②,小明在此基础上进行了深入思考.把等腰三角形ABC换为一般的锐角三角形,其中AB>AC,其它条件不变,小明发现的上述结论还成立吗?请说明理由.
(3)深入研究:
如图③,小明在(2)的基础上,又作了进一步的探究.向△ABC的内侧分别作等腰直角三角形ABD,ACE,其它条件不变,试判断△GMN的形状,并给与证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y=![]() (k≠0,x>0)的图象经过顶点C、D,若点C的横坐标为5,BE=3DE,则k的值为______.
(k≠0,x>0)的图象经过顶点C、D,若点C的横坐标为5,BE=3DE,则k的值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据以下信息,解答下列问题.

(1)小华同学设乙型机器人每小时搬运xkg产品,可列方程为 .
小惠同学设甲型机器人搬运800kg所用时间为y小时,可列方程为 .
(2)请你按照(1)中小华同学的解题思路,写出完整的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,对角线AC,BD交于点O,E是边AD上的一个动点(与点A,D不重合),连接EO并延长,交BC于点F,连接BE,DF.下列说法:
① 对于任意的点E,四边形BEDF都是平行四边形;
② 当∠ABC>90°时,至少存在一个点E,使得四边形BEDF是矩形;
③ 当AB<AD时,至少存在一个点E,使得是四边形BEDF是菱形;
④ 当∠ADB=45°时,至少存在一个点E,使得是四边形BEDF是正方形.
所有正确说法的序号是:_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】再读教材:宽与长的比是![]() (约为0.618)的矩形叫作黄金矩形.黄金矩形给我们以协调、匀称的美感,世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计.下面,我们用宽为2的矩形纸片折叠黄金矩形(提示:
(约为0.618)的矩形叫作黄金矩形.黄金矩形给我们以协调、匀称的美感,世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计.下面,我们用宽为2的矩形纸片折叠黄金矩形(提示:![]() ).
).
第一步:在矩形纸片一端 ,利用图1的方法折出一个正方形,然后把纸片展平;
第二步:如图2,把这个正方形折成两个相等的矩形,再把纸片展平;
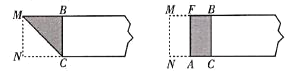
图1 图2
第三步:折出内侧矩形的对角线![]() ,并把
,并把![]() 折到图3中所示的
折到图3中所示的![]() 处;
处;
第四步:展平纸片,按照所得的点![]() 折出
折出![]() ,使
,使![]() ,则图4中就会出现黄金矩形.
,则图4中就会出现黄金矩形.
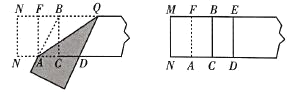
图3 图4
(1)在图3中![]() _________ (保留根号);
_________ (保留根号);
(2)如图3,则四边形![]() 的形状是_________;
的形状是_________;
(3)在图4中黄金矩形是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
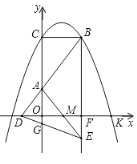
【题目】如图,![]() 与
与![]() 轴交于点C,与
轴交于点C,与![]() 轴的正半轴交于点K,过点
轴的正半轴交于点K,过点![]() 作
作![]() 轴交抛物线于另一点B,点
轴交抛物线于另一点B,点![]() 在
在![]() 轴的负半轴上,连结
轴的负半轴上,连结![]() 交
交![]() 轴于点A,若
轴于点A,若![]() .
.
(1)用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(2)当![]() 时,判断点
时,判断点![]() 是否落在抛物线上,并说明理由;
是否落在抛物线上,并说明理由;
(3)过点![]() 作
作![]() 轴交
轴交![]() 轴于点
轴于点![]() 延长
延长![]() 至
至![]() ,使得
,使得![]() 连结
连结![]() 交
交![]() 轴于点
轴于点![]() 连结AE交
连结AE交![]() 轴于点
轴于点![]() 若
若![]() 的面积与
的面积与![]() 的面积之比为
的面积之比为![]() 则求出抛物线的解析式.
则求出抛物线的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com