
【题目】在平面直角坐标系中,A、B、C三点的坐标分别为:A(1,4)、B(0,3)、C(3,0),若P为x轴上一点,且∠BPC=2∠ACB,则点P的坐标为_____.
【答案】(﹣4,0)或(4,0).
【解析】
由已知可得△ABC是直角三角形,作△ABC关于BC的轴对称图形,得到△BCN,过点A作AM⊥NC,由三角形ANC面积关系,可得![]() AMNC=
AMNC=![]() 2ABBC,AM=
2ABBC,AM=![]() ,MC=
,MC=![]() ,tan∠ACN=tan2∠ACB=
,tan∠ACN=tan2∠ACB=![]() ,tan∠BPC=
,tan∠BPC=![]() ,所以OP=4.
,所以OP=4.
解:如图,∵A(1,4)、B(0,3)、C(3,0),
∴AB=![]() ,BC=3
,BC=3![]() ,AC=2
,AC=2![]() ,△ABC是直角三角形,∠ABC=90°,
,△ABC是直角三角形,∠ABC=90°,
作△ABC关于BC的轴对称图形,得到△BCN,过点A作AM⊥NC,
由三角形ANC面积关系,可得
![]() AMNC=
AMNC=![]() 2ABBC,
2ABBC,
∴2![]() AM=2×
AM=2×![]() ×3
×3![]() ,
,
∴AM=![]() ,
,
∴MC=![]() ,
,
∴tan∠ACN=tan2∠ACB=![]() ,
,
∵∠BPC=2∠ACB,
∴tan∠BPC=![]() ,
,
∴PO=4,
∴P(﹣4,0)或P(4,0),
故答案为(﹣4,0)或(4,0).



科目:初中数学 来源: 题型:
【题目】在初中阶段的函数学习中,我们经历了“确定函数的表达式一一利用函数图象研究其性质一一运用函数解决问题”的学习过程.在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.同时,我们也学习了绝对值的意义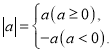 结合上面经历的学习过程,现在来解决下面的问题:在函数
结合上面经历的学习过程,现在来解决下面的问题:在函数![]() 中,当
中,当![]() 时,
时,![]() .
.
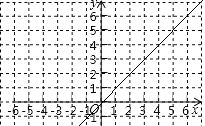
(1)求这个函数的表达式;
(2)在给出的平面直角坐标系中,请用你喜欢的方法画出这个函数的图象并写出这个函数的一条性质;
(3)已如函数![]() 的图象如图所示,结合你所画的函数图象,直接写出不等式
的图象如图所示,结合你所画的函数图象,直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
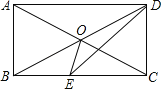
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC,对角线AC、BD交于点O,AO=BO,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若AB=2,求△OEC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如表:
原进价(元/张) | 零售价(元/张) | 成套售价(元/套) | |
餐桌 | a | 270 | 500元 |
餐椅 | a﹣110 | 70 |
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)求表中a的值;
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售.请问怎样进货,才能获得最大利润?最大利润是多少?
(3)由于原材料价格上涨,每张餐桌和餐椅的进价都上涨了10元,但销售价格保持不变.商场购进了餐桌和餐椅共200张,应怎样安排成套销售的销售量(至少10套以上),使得实际全部售出后,最大利润与(2)中相同?请求出进货方案和销售方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
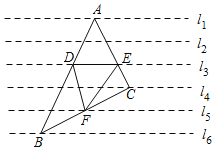
【题目】如图,一组等距的平行线,点A、B、C分别在直线l1、l6、l4上,AB交l3于点D,AC交l3于点E,BC交于l5点F,若△DEF的面积为1,则△ABC的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图AM∥BN,C是BN上一点, BD平分∠ABN且过AC的中点O,交AM于点D,DE⊥BD,交BN于点E.

(1)求证:△ADO≌△CBO.
(2)求证:四边形ABCD是菱形.
(3)若DE = AB = 2,求菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
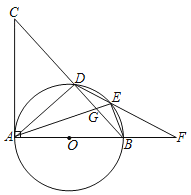
【题目】如图,AB是⊙O的直径,AC⊥AB,BC交⊙O于点D,点E在劣弧BD上,DE的延长线交AB的延长线于点F,连接AE交BD于点G.
(1)求证:∠AED=∠CAD;
(2)若点E是劣弧BD的中点,求证:ED2=EGEA;
(3)在(2)的条件下,若BO=BF,DE=2,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受国内外复杂多变的经济环境影响,去年1至7月,原材料价格一路攀升,长沙市某服装厂每件衣服原材料的成本y1(元)与月份x(1≤x≤7,且x为整数)之间的函数关系如下表:
月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
成本(元/件) | 56 | 58 | 60 | 62 | 64 | 66 | 68 |
8至12月,随着经济环境的好转,原材料价格的涨势趋缓,每件原材料成本y2(元)与月份x的函数关系式为y2=x+62(8≤x≤12,且x为整数).
(1)请观察表格中的数据,用学过的函数相关知识求y1与x的函数关系式.
(2)若去年该衣服每件的出厂价为100元,生产每件衣服的其他成本为8元,该衣服在1至7月的销售量p1(万件)与月份x满足关系式p1=0.1x+1.1(1≤x≤7,且x为整数); 8至12月的销售量p2(万件)与月份x满足关系式p2=﹣0.1x+3(8≤x≤12,且x为整数),该厂去年哪个月利润最大;并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设等边三角形的内切圆半径为![]() 外接圆半径为
外接圆半径为![]() ,平面内任意一点
,平面内任意一点![]() 到等边三角形中心的距离为
到等边三角形中心的距离为![]() 若满足
若满足![]() 则称点
则称点![]() 叫做等边三角形的中心关联点.在平面直角坐标系
叫做等边三角形的中心关联点.在平面直角坐标系![]() 中,等边
中,等边![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() .
.
(1)①等边![]() 中心的坐标为 ;
中心的坐标为 ;
②已知点![]() 在
在![]() 中,是等边
中,是等边![]() 的中心关联点的是 ;
的中心关联点的是 ;
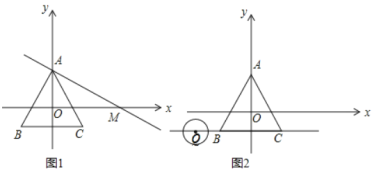
(2)如图1,过点![]() 作直线交
作直线交![]() 轴正半轴于
轴正半轴于![]() 使
使![]() .
.
①若线段![]() 上存在等边
上存在等边![]() 的中心关联点
的中心关联点![]() 求
求![]() 的取值范围;
的取值范围;
②将直线![]() 向下平移得到直线
向下平移得到直线![]() 当
当![]() 满足什么条件时,直线
满足什么条件时,直线![]() 上总存在等边
上总存在等边![]() 的中心关联点;
的中心关联点;
(3)如图2,点![]() 为直线
为直线![]() 上一动点,
上一动点,![]() 的半径为
的半径为![]() 当
当![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度向右移动,运动时间为
个单位的速度向右移动,运动时间为![]() 秒.是否存在某一时刻
秒.是否存在某一时刻![]() 使得
使得![]() 上所有点都是等边
上所有点都是等边![]() 的中心关联点?如果存在,请直接写出所有符合题意的
的中心关联点?如果存在,请直接写出所有符合题意的![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com